All published articles of this journal are available on ScienceDirect.
Realizing the Effective Detection of Tumor in Magnetic Resonance Imaging using Cluster-Sparse Assisted Super-Resolution
Abstract
Recently, significant research has been done in Super-Resolution (SR) methods for augmenting the spatial resolution of the Magnetic Resonance (MR) images, which aids the physician in improved disease diagnoses. Single SR methods have drawbacks; they fail to capture self-similarity in non-local patches and are not robust to noise. To exploit the non-local self-similarity and intrinsic sparsity in MR images, this paper proposes the use of Cluster-Sparse Assisted Super-Resolution. This SR method effectively captures similarity in non-locally positioned patches by training on clusters of patches using a self-adaptive dictionary. This method of training also leads to better edge and texture detection. Experiments show that using Cluster-Sparse Assisted Super-Resolution for brain MR images results in enhanced detection of lesions leading to better diagnosis.
1. INTRODUCTION
Medical imaging is a safe and reliable method for disease detection and diagnosis. There are various medical imaging techniques employed in clinical practice like Computed Tomography (CT), Positron Emission Tomography (PET), Magnetic Resonance Imaging (MRI) to name a few. These techniques provide various functional and anatomical information and that too at varied temporal and spatial resolutions [1]. A high-resolution medical image is a key to better medical research or diagnosis and treatment
However, due to physical and hardware constraints, the images produced by the above-mentioned imaging techniques are of low resolution and are noisy; this negatively affects medical research and diagnosis [2]. Improving the imaging hardware to get better quality images is expensive and not a viable option.A potential solution is to use the Low Resolution (LR) image produced by the imaging techniques and produce a High-Resolution (HR) image using appropriate techniques. This HR image can lead to an accurate image analysis giving a better clinical diagnosis. SR is an appealing method which does exactly the same; it takes an LR image and yields an HR image. However, the undetermined nature of SR makes it a challenging problem to solve [3]. A huge amount of HR images, when decimated, produce LR images, this makes it difficult to restore accurate details from the LR image, moreover, most SR methods are a convex optimization problem and it is cumbersome to balance the regularization terms while simultaneously yielding high-resolution images [4]. Contrary to traditional methods, which uses just a single LR image, Liang et al. [5], used a sequence of images, assuming that there were no changes in imaging conditions (focal length, lighting, etc.) [6]. However, that is not the case and the performance of the SR method is affected by changes in imaging conditions in each image of the sequence. Using the process of SR, an HR image can be obtained from an LR image. However, this method assumes that the previous knowledge of restoration is known i.e. the impulse response (point spread function) of the system is known. Moreover, in the majority of the cases, this point spread function is not known. Current research has made some improvements in the usage of this method but these improvements are not very significant and the applications are still limited.
Jeong et al. used a fuzzy system in SR image estimation. The PSF (Point Spread Function) was assumed to be a circle and for the degeneration matrix, a cyclic square matrix was employed [7]. In a study by Alqadah et al., Linear Spatial Invariant (LSI) was used to deal with PSF and Gaussian Quadratic Criterion and Lanczos algorithm was used to approximate the values of the fuzzy parameters [8]. Herment et al. pioneered SR in MRIs, and the images were reconstructed using k space data with the help of 3-D MRI volumes [9, 10]. However, the lack of isotropic resolution leads to poor results for brain MRI. Peeled and Yeshurun applied IBP algorithm for SR and used LR diffusion tensor images for MRI [11]. Scheffler negated this result [12] and Greenspan further verified it using 2-D multi-slice MRI scans and applied SR on them [13]. SR was used on functional MRI data by Peeters et al. [14]. In a functional MRI, the temporal activity is visible. An additive model was used to compute the shared space from the pixel of LR and HR image
Carmi et al. further explored the application of SR in MRI data by using a novel sampling condition [15]. They used uniform spatial shifts and equal sampling in LR images and with this, they managed to propagate the global spatial errors in the SR reconstructed HR image. Bai et al. further improved the resolution of MRI brain images by using combinations of orthogonal scans of the same subject [16], the MAP function devised by Hardie et al. was used for this purpose [17]. For SR reconstruction, nearest neighbours and interpolation-based methods like linear interpolation can also be used [18, 19]. However, it becomes difficult to preserve edge and texture when using this method thus leading to blurred edges and textures. Lu et al. explored learning-based methods for SR reconstruction of MRI images [20, 21]. Using the HR T-1 weighted image, the intra-patient information is extracted which is used to guide the SR process. Further, an LR T-2 weighted image can be constructed by using an extension of the previously mentioned method along with dictionary learning and a sparse representation
1.1. Key Contributions of this Research
MRI is a non-invasive imaging technology used for disease detection and treatment monitoring [20]. Even though imaging technology is sophisticated, the various processes the image undergoes, like transmission and storage tend to introduce noise in the image. This leads to a loss in the quality of the image which means loss of crucial medical information resulting in poor diagnosis. Super-resolution is a method which can produce an HR image from its corresponding LR image. In recent years there has been significant research into SR methods for MR image-based diagnosis. However, there are still some problems with single super-resolution techniques. Such techniques are not robust to noise since they fail to perform de-noising and SR simultaneously, moreover, such techniques also assume that an LR image is obtained by decimating its corresponding HR image. This paper focuses on cluster-sparse assisted super-resolution technique (CSR), which can overcome the drawback of single SR techniques and other restoration dependent techniques. The key features of CSR are that it is robust to noise and exploits non-locally positioned similar patches. CSR also leads to better edge and texture detection because the dictionary employed by the method is trained on a cluster of patches instead of a single patch, also the dictionary being used is not a general dictionary, instead, and a self-adaptive dictionary is being used. All these features together offer enhanced detection of lesions leading to better diagnosis [22-25].
2. RELATED WORK
Many recent approaches have been proposed in the domain of automatic diagnosis of brain tumor detection via MRI using machine learning and computer vision. Jose et al. [26] work was one of the first articles which analysed and showed how super resolution could affect the detection of tumor in MRI. They tried to highlight that in MRI typical clinical settings, both low- and high-resolution images of different types are routinely acquired, out of which we can leverage the low resolution imaging by using super resolution imaging techniques. The method suggested reconstructing high resolution images from the low resolution images using information from coplanar high resolution images acquired from the same subject. A work by Plenge et al. [27] also performed a prodigious study on the trade-off between resolution, signal-to-noise ratio and acquisition time. Qualitative experiments were performed, in which they took images of three different subjects using MRI, and the results showed that super-resolution reconstruction was indeed improving the resolution, signal-to-noise ratio and acquisition time trade-offs compared with direct high resolution acquisition. Francois et al. [28] established a supervised patch based image reconstruction technique for to brain MRI super-resolution. They considered a supervised regularization technique that was driven by the similarities between the input image and learning data-set. The similarities were computed using patch based approach and were defined at the voxel scale.
Similar method was devised by Ali et al. [29], where they used a similar super resolution process, for developing a novel technique, which enabled the reconstruction of a volumetric image from multiple-scan slice acquisitions. The technique tries to generate a super resolution of the Fetal Brain MRI volumetric scan. Yun-Heng et al. [30] were the first ones to develop and propose a sparse representation-based super resolution reconstruction for MRI. Their framework as presented was mainly built for the reasons to solve the data collection limitations. They proposed a novel dictionary training method through sparse reconstruction for enhancing the similarity between the sparse representations of low and high resolution MRI block pairs by simultaneously training both the dictionaries. They proposed a new set of sparse representation coefficients, which were used to generate high resolution MRI blocks from the low resolution MRI blocks.
For recent studies, few deep learning based techniques have also been proposed towards this goal. Since, neural networks have shown us how they work better and perform better in accuracy. Chi-Hieu et al. [31], had established a novel deep 3-D convolutional network based architecture for brain MRI super-resolution. They had taken the 3-D approach using the normal super-resolution via neural networks where they generate high resolution images from its input low-resolution with help of patches of other HR brain images. Of course, deep learning techniques have come up in recent times and they outperform classical approaches, but they have few drawbacks such as heavy data requirements, a lot of resource requirements such as high end graphics processors and a lot of time required for training, which sometimes takes many days.
A patch based SR framework which utilizes Fourier Burst Accumulation to form the HR image from LR patches was presented by Jog et al. [32]. The usage of conjugated gradient method and a linear system was devised as a method to acquire HR image from LR image by Poot et al. [33]. A two-stage algorithm for MRI SR was explored. According to Ongie et al. [34], an edge mask was obtained in the first stage, and this mask which represents the edges of the image was used as an image prior to the second stage. The use of Tikhonov regularization for MRI SR in slice-select direction was explored by Zhang et al. in [35]. The Property of self-similarity that is intrinsically present in MRI was utilized along with image priors by Manjon et al. in [36]. Iterative motion correction and HR image estimation was explored for HR fetal brain MRI by Rousseau et al. [37].
SR algorithms which involve sparse coding comprise the use of dictionaries, and it is a key area of research, in these algorithms the efficiency of learning were improved by using these dictionaries. Yang et al. [38] established a method for SR using clustered sparse encoding and learned geometric dictionaries for super-resolution of LR images. Zheng et al. in [39] presented an approach to SR where multiple dictionaries were deployed. Also, a novel dictionary selection method was presented in this work. These dictionaries were then used to generate sparse representation of LR images which was then used to reconstruct the HR image. The concept of sparse coding noise was introduced in [40] by Dong et al., in this method for SR, the objective of restoring the image was defined as suppressing the sparse coding noise. A SR method which preserves image edges was presented in [41] by Huang et al., this edge preserving smoothing was accomplished by using EPS regularization term. A hierarchical and sparse representation for SR image was devised by Liu et al. in [42]. They combined both clustering and collaboration to code the image. Clustering was used to cluster the feature space of an image into multiple LR feature. Collaborative representation was used to map the LR feature subspace to the HR subspace. Another clustering based method for SR was presented by Han et al. in [43]; here the optimal representation problem was solved using jointly-low rank and sparse regularization for each subspace.
In multi-dictionary learning, an important task was to choose the correct dictionary, for this Wei et al. presented the random forest technique, to learn the most suitable dictionary for each patch [44]. A sparse neighbour encoding and a sparse neighbour selection scheme was presented by Gao et al. [45]. A directionally structured coupled dictionary learning was established by Ahmed et al. [46], whereas a semi-coupled dictionary learning for SR was presented by Wang et al. [47]. In both cases, a pair of dictionaries and mapping functions were deployed. Sivakumar et al. presented a method for denoising of MRI using curvelet transform [20].
However, there exists an insufficient amount of work towards using modified sparse representation techniques in the domain of brain tumor detection in MRI. To the best of our understanding, this is the first work to report a cluster-sparse representation based solution for diagnosing the tumor in MRI.
3. MATERIALS AND METHODS
There has been a lot of research and attempts at restoring a high-resolution image (x) from its degraded low-resolution image (y). This can be mathematically expressed as
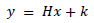 |
(1) |
The images x and y are represented using lexicographic matrices, the degradation operator is H and the Gaussian white noise is represented by k. The value of H determines the type of image restoration. This scenario is expressed as a minimization problem.
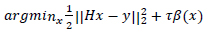 |
(2) |
The l2 fidelity is 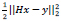 and the regularization parameter for image prior is β(x).
and the regularization parameter for image prior is β(x).
Traditional models assume that except for the edges, the image is locally smooth. This assumption leads to inaccurate restoration resulting in the loss of finer details in the reconstructed image. Previous research has indicated that natural images intrinsically have the property of sparsity. This fact can be utilized to represent images using sparse models. In such models, a small sample of elements can be used from a basis set stored in a dictionary. Previously models used wavelets and bandlets which are traditional dictionary sets; however, using a learned dictionary can yield better results. Moreover, these traditional models fail to exploit the similarity that exists between non-local patches. Some methods use weighted graphs to identify textures and other high-level patterns, however, inaccurate weights can lead to loss of details in the reconstructed image.
This research paper introduces Cluster-Sparse assisted Super Resolution technique (CSR), a superior method for restoration of the MR images [22]. This method can effectively exploit the similarity in the non-local patches (non-local self-similarity) and the local sparsity, which is intrinsically present in natural images. An iterative algorithm based on Split Bregman method coupled with self-adaptive cluster dictionary learning method is used for image restoration.
3.1. Traditional Approach
In the traditional approach, the image is divided into n patches denoted by XK where k = 1,2,..,n and k is also an indicator of the position of the patch in the image. An operator is used to extract XK from the image, this operator is denoted by  . The image patch is expressed as
. The image patch is expressed as
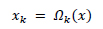 |
(3) |
To replace the patch back to its former position in the reconstructed image 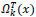 is used. This is nothing but the transpose of the function
is used. This is nothing but the transpose of the function 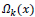 .
.
D Ɛ RB s* M is used to yield a sparse representation for each patch Xk in form of a sparse vector αkƐRM such that 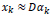 . Here the number of atoms in D is denoted by M. The scenario above can be mathematically expressed as
. Here the number of atoms in D is denoted by M. The scenario above can be mathematically expressed as
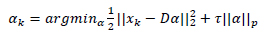 |
(4) |
In the above equation, the norm used to measure sparsity is determined by p such that pƐ{0,1} and τ is a constant. The above equation is solved using Orthogonal Matching Pursuit (OMP) [23] which is a greedy algorithm.
The following expression represents the degradation based sparsity approach
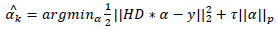 |
(5) |
The altered and reconstructed image is
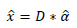 |
(6) |
High complexity approximation approaches are used to make dictionary learning feasible since training a proper dictionary is a non-convex problem
3.2. CSR Approach
In this approach, instead of using patches, a cluster of patches is used for training the dictionary. Sparse representation of clusters is used to capture the similarity present in non-local patches, a task which traditional methods failed to do. Fig. (1) illustrates the CSR approach for cluster creation from the MR Imagery x.
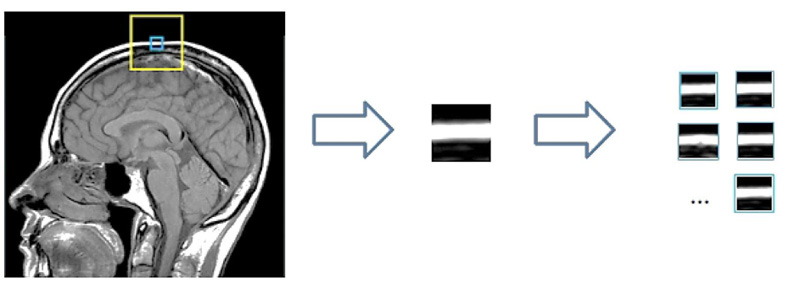
The image x of size N is divided into patches Xk where x = 1,2,...,n such that the size of xk is 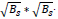 . Now in L * L training window, the top c matches for a patch are selected. These c best-matched patches for a patch xk are stored in a set Sx. The patches in Sx, are stored in a matrix XGK such that
. Now in L * L training window, the top c matches for a patch are selected. These c best-matched patches for a patch xk are stored in a set Sx. The patches in Sx, are stored in a matrix XGK such that 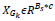 .
.
A function to extract a cluster XGK from image is defined as:
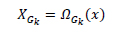 |
(7) |
To replace the patch back to its former position in the reconstructed image 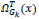 is used. This is again nothing but the transpose of the function
is used. This is again nothing but the transpose of the function 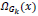 .
.
In the traditional method, a general dictionary was used to improve efficiency a self-adaptive dictionary was used. This self-adaptive dictionary is trained using the formula,
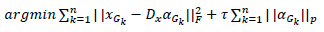 |
(8) |
Similar to the formula in the traditional method, the norm used to measure sparsity is determined by p such that pƐ{0,1} and τ is a constant.
In the above expression, there are two parameters which need to be optimized Dx and {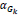 } hence the problem is a joint optimization problem. When the similarity between the reconstructed image and the original image is high, then the value of
} hence the problem is a joint optimization problem. When the similarity between the reconstructed image and the original image is high, then the value of 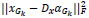 will be low, while the value of the second term
will be low, while the value of the second term 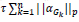 will be low when
will be low when 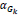 is very sparse.
is very sparse.
The clusters will be reconstructed using the self-adaptive dictionary. The dictionary is solved using the SVD approach where both Dx and {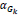 } are alternatively optimized. The CSIR model using degraded version is represented as:
} are alternatively optimized. The CSIR model using degraded version is represented as:
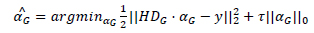 |
(9) |
And the reconstructed image is expressed as:
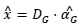 |
(10) |
The main difference between the model in the traditional approach and the model in the CSIR approach is the different dictionaries being used and the different sparse representations
Iterative shrinkage/thresholding (IST) was used in earlier models to solve the problem but this study adopts a split Bregman Iteration (SBI) [24].
3.3. Experimental Results
The MR image of the human brain is iteratively enhanced in quality using the CSR approach. A Gaussian blur kernel and a 9x9 kernel along with additive noise of 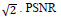 comparison is used as the metric to compare the efficiencies of both, the traditional approach and the CSR approach. PSNR is expressed as for given two images I and J.
comparison is used as the metric to compare the efficiencies of both, the traditional approach and the CSR approach. PSNR is expressed as for given two images I and J.
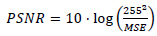 |
(11) |
Here MSE is the mean squared error and is defined as:
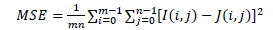 |
(12) |
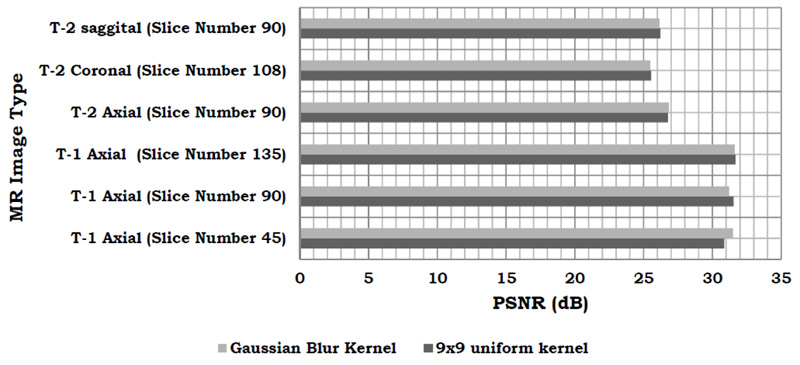
The results of the PSNR comparison show that both the kernels yield similar results and Fig. (2) shows a graphical comparison of the same.
| MRI\ Method | CSR Method | Non-Local Means | Bicubic Interpolation | Nearest Neighbour Interpolation |
|---|---|---|---|---|
| T-1 Axial | 30.8592 | 22.2218 | 25.9786 | 21.0829 |
| T-1 Axial | 31.5304 | 22.1411 | 25.6068 | 20.9554 |
| T-1 Axial | 31.6757 | 22.1830 | 26.0537 | 20.8869 |
| T-2 Axial | 26.7767 | 18.6923 | 22.0170 | 17.6479 |
| T-2 Coronal | 25.5359 | 18.1610 | 21.9001 | 17.4234 |
| T-2 Sagittal Axial | 26.2216 | 18.4218 | 22.1784 | 17.6759 |
Comparison between the CSR algorithm proposed in this study and other methods which take an approach based on non-local means, nearest neighbour and bicubic interpolation has been done. For this comparison, a 9x9 uniform kernel has been utilized. The PSNR values give a measure of the effectiveness of the different algorithms under consideration (Table 1). Further, Table 2 presents the comparison of the various state-of-the art (SOTA) techniques for Brain MRI Super-resolution.
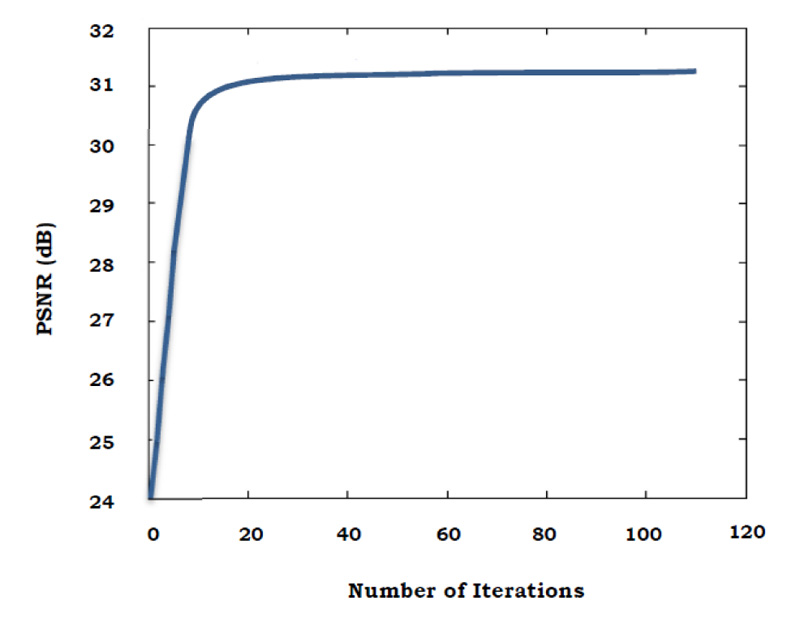
The graph below shows the relation between PSNR value and the number of iterations, where in the PSNR value increases with every iteration (Fig. 3).
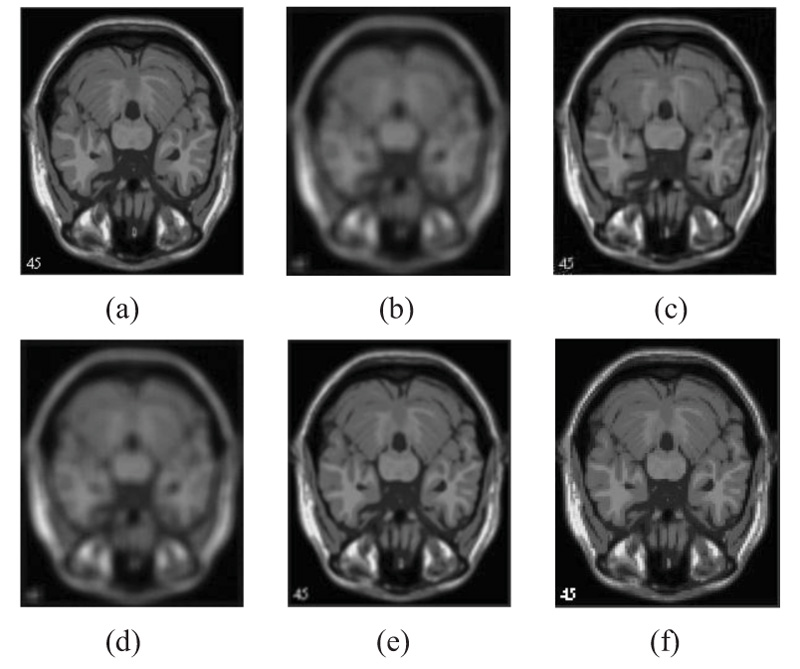
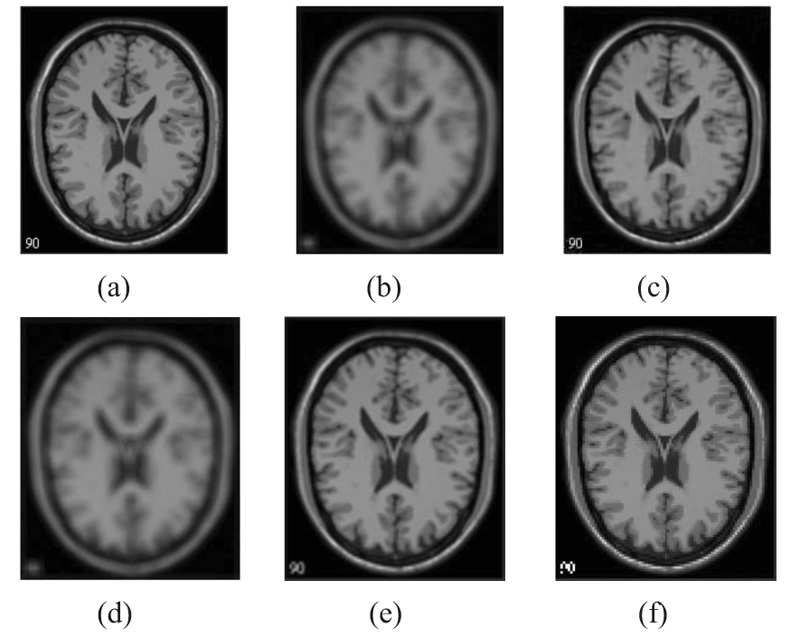
The two forms of MR T1 and T2-w brain MS lesion images [25] (Figs. 4-9) are used for evaluating the reconstructed images using CSR and other methods mentioned.
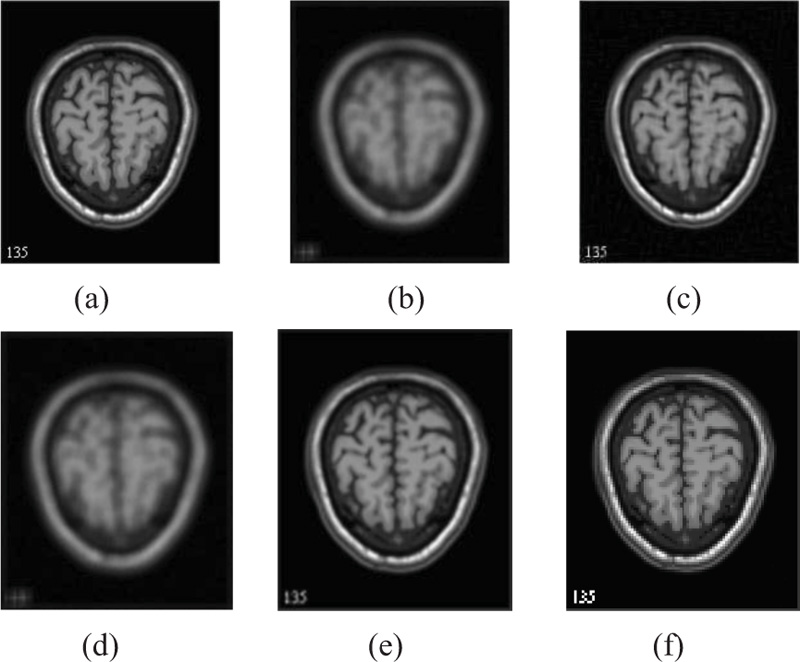
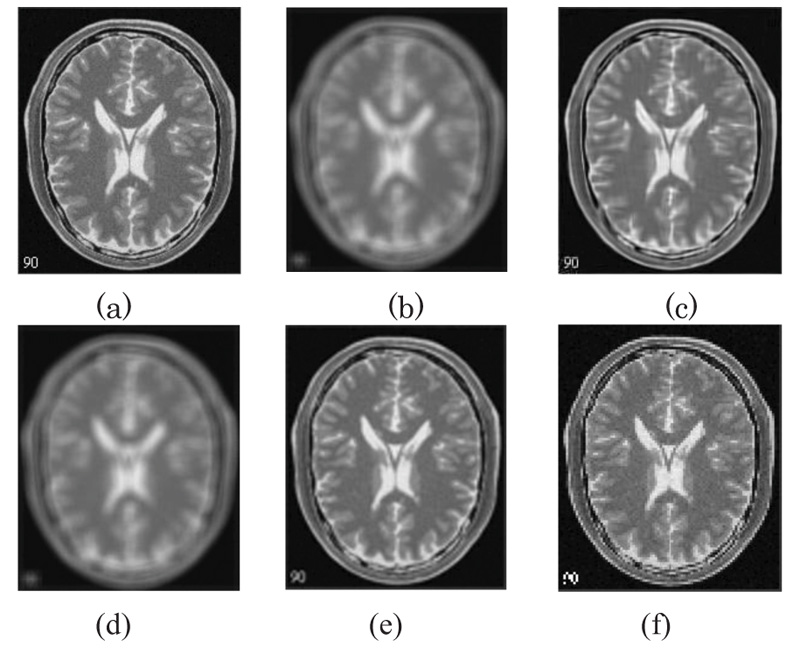
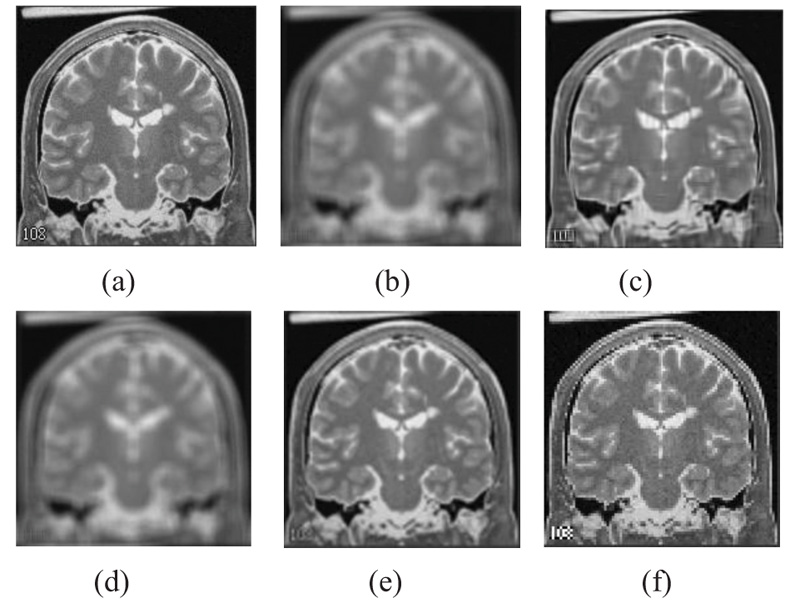
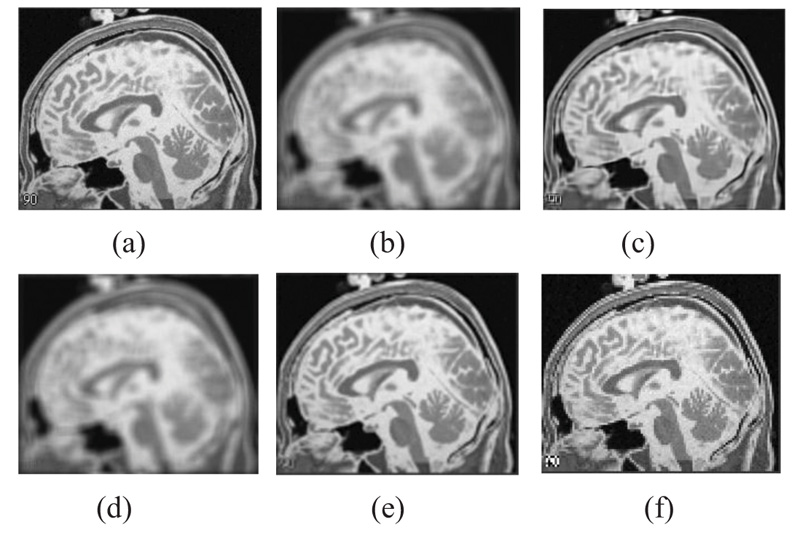
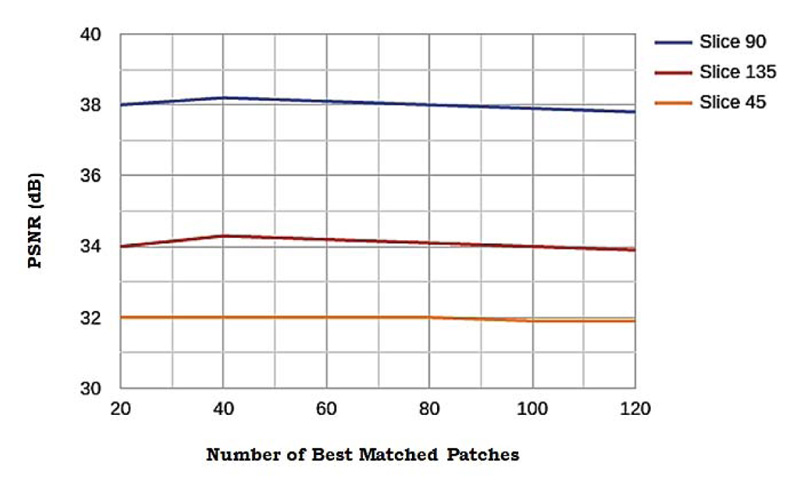
3.4. Influence of Number of Best-matched Patches
The influence of ci.e. the number of best-matched patches on the sensitivity of the performance is elucidated in this subsection. An experiment was conducted to explore this, various values of c, from 20 to 120 were sampled and three tests were taken. Fig. (10) shows the comparison of the performance along with the value of c. The flat curves in Fig. (10) indicates that the algorithm is not sensitive to the value of c. In this study, the value of c is set to 60 as experiments yielded the highest performance for c in the range of 40 to 80.
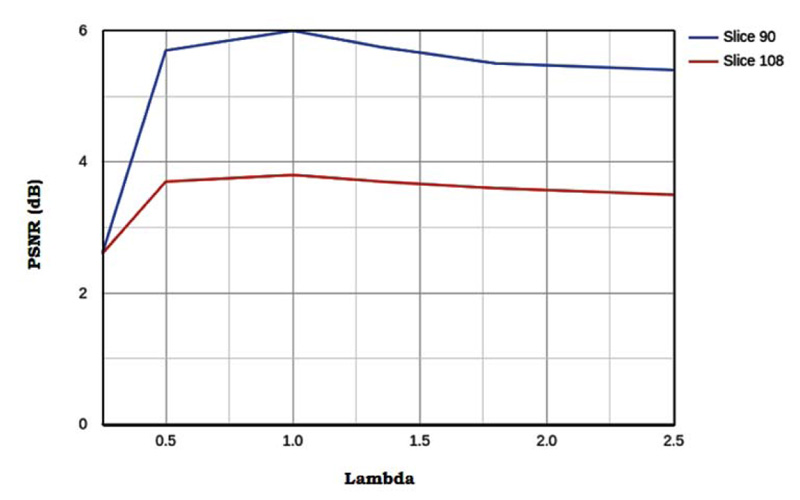
3.5. Effect of Sparsity Parameter
By observing Fig. (11), we can conclude the following 2 things. There exists an optimal λ for which the image noise suppression is balanced with image details preservation such that PSNR is the highest. A large value of λ leads to loss of details and a small value causes the failure in suppressing the image noise. Thus the optimal value for each test image is same, this helps in parameter optimization as the optimal value of λ can be determined using a single test image and this λ can be further used for all the other test images. λ and δ are correlated to each other. A large δ leads to a large λ
CONCLUSION
This paper proposes the use of cluster-sparse assisted super-resolution algorithm for Magnetic resonance (MR) images. This algorithm captures the similarity in non-local patches by training the model for clusters instead of patches using a self-adaptive dictionary. This type of training using clusters also leads to better edge and texture retention in the reconstructed image. The experimental results show that the proposed algorithm is more robust to noise and is more effective in producing high-resolution images than traditional SR methods dealing with MR images.
As a result, usage of this algorithm can lead to more effective information extraction from MR images in medical diagnosis and research leading to enhanced detection of lesions.
The current trend in MR image super-resolution involves using deep learning approaches. Convolutional neural networks are used to develop end-to-end image super-resolution model, where various convolution kernels extract features from LR input image to form a feature map, this feature map is used to generate HR images. More recently, Generative Adversarial Networks (GANs) have been used for MR image SR. GANs learn to generate realistic HR image from LR image input, such that the generated HR image is hardly distinguishable from real HR images. However, deep neural networks consume a lot of memory and take a lot of time to compute. Training of these models and inference using them is heavily constrained by the availability of graphical processing units for mathematical computations [47-54].
CONSENT FOR PUBLICATION
Not Applicable
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
FUNDING
None.
ACKNOWLEDGEMENTS
Declared none.


