Grid Search based Optimum Feature Selection by Tuning hyperparameters for Heart Disease Diagnosis in Machine learning

All published articles of this journal are available on ScienceDirect.

RESEARCH ARTICLE

Grid Search based Optimum Feature Selection by Tuning hyperparameters for Heart Disease Diagnosis in Machine learning

G. Saranya1 , * Open Modal A. Pravin2
Authors Info & Affiliations
The Open Biomedical Engineering Journal • 17 May 2023 • RESEARCH ARTICLE • DOI: 10.2174/18741207-v17-e230510-2022-HT28-4371-8
Previous Article

Abstract

Background:

Heart disease prediction model helps physicians to identify patients who are at high risk of developing heart disease and target prevention strategies accordingly. These models use patient demographics, medical history, lifecycle factors, and clinical measurements to calculate the risk of heart disease within a certain time frame. In identifying important features of heart disease, a popular approach is using Machine learning (ML) models. ML models can analyse a large amount of data and find patterns that are difficult for humans to detect.

Methods:

In this proposed work, Random Forest classifier is used to identify the most important features that contribute to heart disease and increase the prediction accuracy of the model by tuning the hyperparameters using grid search approach.

Results:

The proposed system was evaluated and compared in terms of accuracy, error rate and recall with the traditional system. As the traditional system achieved accuracies between 81.97% and 90.16%., the proposed hyperparameter tuning model achieved accuracies in the range increased between 84.22% and 96.53%.

Conclusion:

These evaluations demonstrated that the proposed prediction approach is capable of achieving more accurate results compared with the traditional approach in predicting heart disease by finding optimum features.

Keywords: Grid search optimization (GSO), Machine learning(ML), Random forest (RF), Hyperparameter tuning, Heart disease, Feature selection (FS).

1. INTRODUCTION

In recent years, data science has contributed a significant role in the healthcare industry by providing better Machine learning tools for predicting chronic diseases. Heart disease is one of the common ailments suffered by ordinary people [1]. According to the World health organization, the mortality rate of heart disease patients is nearly 17.9 million every year, which is a leading death rate worldwide [2]. For diagnosing and building better clinical decision support, ML models can be deployed to mitigate the disease by understanding the symptoms of heart disease based on the relevant feature sets [3]. Machine learning has emerged with practical techniques to make predictions from a large pool of data. Its analytical tool gives a solution when predicting complex diseases like knowledge transformation of medical records, cardiac diseases, and gene data analysis [4-6]. Machine Learning (ML) comprises learning algorithms explored on the existing data to discover the hidden pattern, and the rules of learning models used to predict the occurrence and non-occurrence of the target data, particularly in the research area [7]. This ML algorithm works with noisy data as well. ML model ranks different features depending upon their relevance to the paradigm and assign some weights during the learning process [8-12]. Predominantly ML harnesses both supervised and unsupervised learning methods. The former learning technique produces the best relationship and dependencies between the prediction output and the trained set's input features.

Thus producing predicted output for the new dataset. Though many ML models have been explored [13, 14] and are perhaps successful in their analysis, predicting heart disease emerges as a significant paradigm that needs improved models and methods. This prediction comes under supervised learning using classification techniques to learn the relationship and dependency amidst features and the target class [14-19]. In machine learning, hyperparameter tuning is proclaimed to train the model. The problem dwells in choosing the optimal hyperparameters. In this concern, Random Forest plays a significant role in predicting the target values. RF is an ensemble model constructed from a set of independent and distinct decision trees based on the randomization technique using a random vector parameter that selects the features randomly in the training set [20-22]. Generally, the feature selection technique handles high dimensional dataset [23] that requires huge memory leading to an overfitting problem. Weighted features can be selected to improve model performance and reduce processing time [24-31]. Thus selecting a small number of relevant features reduces the dimension of the data set using feature selection [32] and extraction by transforming and removing unwanted data using Grid optimization methods.

In the proposed model, the motivation of this work is to identify the essential features by tuning the hyperparameters during feature selection and improving the performance of the classifiers deploying grid search methods. Optimal parameters are chosen during the tuning process and thus predicting heart disease.

The contribution of the proposed work is listed below:

  • Three grid search methods, such as best-random, first grid, and second, are constructed in the initial phase.
  • In the second phase, the hyperparameter tuning process is carried out with Grid search and random search models by fixing the baseline parameters.
  • In the third phase, the feature extraction and feature selection process with the cross-validation method is implemented.
  • After selecting optimal parameters, the best model is determined by validating with parameters such as runtime, mean error, and accuracy.
  • In the final phase, the classification accuracy of the RF model is enhanced with the best grid model.

2. LITERATURE SURVEY

The authors proposed deep learning methods, Logistic regression, SVM and RF models. They explored the heart disease data by tuning the hyperparameter with relevant feature selection and producing more than 78% accuracy [33].

They have proposed generalized discriminant analysis (GDA) to classify 15 features with an HRV signal. The features have been reduced to 5 sets using the GDA model and produced a 100% precision result with an SVM classifier [34].

An effective technique to speed up the performance of the model by hyperparameter tuning using Grid search implemented on text data with a kNN algorithm. The model is tuned with three parameters using BM25 similarity [35].

Authors implemented the Naïve Bayes algorithm to predict heart disease patients and proposed a novel Heart Disease Prediction System (HDPS) system [36-38]. The author has examined specific parameters and predicted Heart disease by deploying a K-mean clustering algorithm [39].

Bayesian hyperparameter optimization algorithm was proposed to improve the model [40]. This Bayesian model is used for hyperparameter tuning that obtains optimized values with less consumption time and performance improvement, thus achieving global optimization.

Authors proposed Enhanced Bat Optimization (EBO) algorithm to select appropriate features from the gene dataset. A subset of significant genes is selected using the bat algorithm associated with Hilbert Schmidt Independence Criterion (HSIC) measure [41].

The authors proposed a system by tuning the hyperparameters to predict heart disease [42]. The performance of the model was enhanced using the grid search approach with five Logistic regression, K-Nearest Neighbor, support vector machine, decision tree, and random forest. The metrics used to evaluate the performance of the algorithms were precision, recall and F1_Score [43-49].

A framework was designed with five algorithms: RF, Naïve Bayes, SVM, Hoeffding DT, and Logistic Model Tree. The heart disease classification was carried out by selecting the best features from the dataset by obtaining 81.24% accuracy [50].

Authors devised a prediction model with a finely tuned technique that identified the key features. A classification model was constructed using RF, SVM and DT models that produced higher predictive accuracy [51].

Researchers proposed a deep learning model using Neural Network (NN) for classifying electrocardiogram(ECG) signals for selecting the relevant set of features and enhancing the performance of the classifier [52].

A clinical decision support system (CDSS) was proposed to analyze heart failure. The author implemented machine learning algorithms like neural network (NN), support vector machine (SVM), classification, and regression. (CART) with fuzzy rules and random forests (RF) and the CART model and RF produced 87.6% accuracy [53].

Authors deployed the SVM model for diagnosing heart disease patients with diabetes. The author obtained 94.60% accuracy by predicting the significant features considering age, blood pressure and sugar [54].

They proposed a cardiovascular feature reduction process by implementing the Fisher ranking method, discriminant analysis (DA), and binary classification with extreme learning method (EML). The model obtained an accuracy of 100% in detecting heart disease [55].

An automatic classification in analyzing cardiac arrhythmia with linear and non-linear with dimensional reduction models under unsupervised learning using a neural network (NN) classifier was carried out and achieved 99.83% of F1-score using fast ICA algorithm with only 10 components [56].

Researchers have made a complete analysis of different feature selection techniques. Various functional issues of feature selection algorithms have been in terms of dimensionality reduction and classification accuracy [57-63]. They demonstrated a new perspective feature selection process from the adaptable reconstruction graph and feature subset [64-69]. Authors minimize the tuning issues of several optimization methods in feature selection-based data analysis by selecting features from Binary Teaching and Learning Optimization technique (BTLO) [70-76] where the size and number of subsets generated are the control variables. They found that the loss of data occurred in a conventional SVM method where feature extraction and parameter tuning were done independently [77]. In order to overcome this, a convex energy dependent system is proposed where the feature selection and parameter tuning are integrated [78].

Authors have initiated an unsupervised feature selection framework for social media data [79]. In this paper, under the unsupervised case, the problems of feature selection in social media data are investigated.

The proposed method increases the model performance by implementing a grid optimization model in a random search using a cross-validation technique. Section 2 elucidates the proposed methodology with three models: best-random using cv method, First-grid with cv and Second-grid. Section 3 exemplifies the results and discussion phase, and section 4 summarizes the proposed method.

3. PROPOSED METHODOLOGY

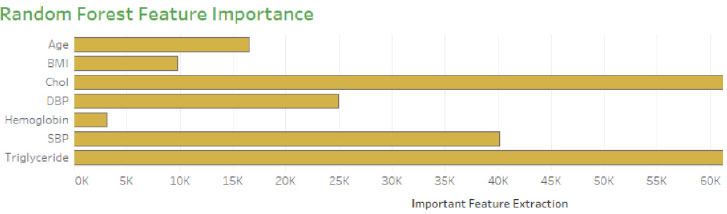
The proposed work is organized with three models for optimal feature selection in predicting heart disease. Feature selection plays a significant role in predicting the disease. The factors that increase the risk of heart disease include triglyceride, high cholesterol [80-83], and American Heart Association [84] indicates that body mass index (BMI), leg swelling, chronic cough and high blood pressure [85]. Feature extraction is carried out by tuning the parameters using the Grid search algorithm to select optimum attributes. The scheduled model is explored on the heart disease dataset (Cleveland dataset) collected from the UCI machine learning repository. The dataset consists of 14 features with 303 instances where 300 instances are taken for analysis. The characteristic features, along with their description and range of values, are outlined in Table 1.

Fig. (1). The architecture of the proposed method.
Table 1.
Characteristics of cleveland dataset.
Features Description Ranges
Age Age (in years) 30–92
Sex Gender 1: male; 0: female
BMI Body mass index 15.302–41.304
Cholesterol Blood Cholesterol level 79–525
HDL High-Density Lipoprotein 22–118
SBP Systolic blood Pressure 75–219
DBP Diastolic blood Pressure 10–137
Triglyceride Teen’s body fat 20–1868
Haemoglobin Haemoglobin 7–19
TD Thyroid disease Categorical – yes, no
CRF chronic renal failure Categorical – yes, no
Cirrhosis Cirrhosis Categorical – yes, no
Smoking Smoking habit Categorical – yes, no

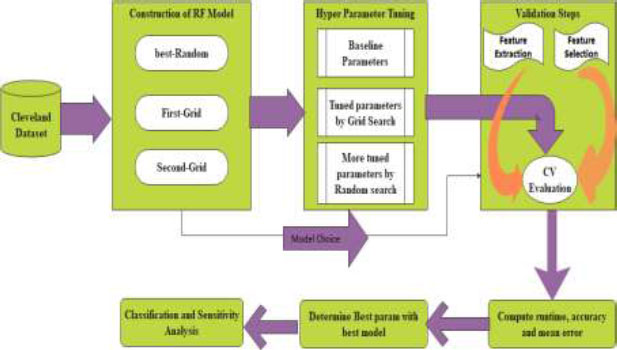
The relevant (important features) from the dataset are extracted during the grid search, and the model is trained using hyperparameters to perceive the optimal model. The schemed model contemplates recall measure, and the model is trained to reduce the false-negative rate during classification using the Random Forest. The method is designed with three phases. 1. Construction of RF Model 2. Hyperparameter Tuning 3. Validation phase. The architecture of the prompted framework is delineated in Fig. (1). Three models are validated with cross-validation to extenuate the overfitting paradigm. The average accuracy, average error, runtime, validation score, and train time are computed for all three models for determining the best parameters from the best model to increase the recall ratio during classification.

3.1. Construction of RF Model

Random Forest (RF) is an ensemble learning model for classification and regression constructed using multiple decision trees. Bootstrap is employed to maximize the diversity of each tree. In RF, each decision tree is trained. Let the training set is taken as Td = {(x1, y1), (x2, y2) …. (xn,yn)}. Td is the training data for each decision tree Dt and let E(x) represents the estimation result on sample x then,

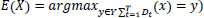(1)

Each node in the bootstrap tests the particular features, and finally, the leaf node represents the output. The aggregated results of all bootstrap sets are expressed as:

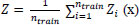(2)

Where Z is the average output of n trees, Zix , is the corresponding prediction for the input x. The number of trees is split into 100,200, 300 from the Cleveland dataset in the proposed model. After splitting trees into binary nodes, the splits are investigated to remove the impurities from the resulting tree, and the optimal split is selected. This splitting is done as follows:

(3)

Where sldenotes the split portion at node t, ∆ipsl,t represents the impurity reduction measure, ipt denotes the occurrence of impurity before splitting the training dataset and iTl -iTr represents the impurities after splitting between both the left node and right node with the proportion pr. The proposed work is framed with three models. Best-random from random search with cross-validation, First-grid search with cross-validation and Second-grid search. In the first design pattern model, the randomized search is proclaimed using the cross-validation method, where 7 essential features are selected from 14 features Fig. (2) by defining the ranges and sampling randomly from the grid with 5 fold CV for each combination of the sample. A randomized parameter grid is created to sample from the distribution during fitting. The proposed model is compared with the base model using the test features and predictions to determine whether the random search has yielded a better result. Similarly, the other two models are also constructed in the meantime and evaluated using the base model.

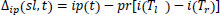3.2. Hyperparameter Tuning

In the proposed work, a hyperparameter is used to set before training the model. For Random Forest classification, four parameters such as the number of trees, depth of the tree, a minimum number of samples and the minimum number of samples present at leaf node shown in Fig. (3). These parameters are adjusted to determine which features to modify or retain from the dataset and those features are extracted after tuning. Initially, baseline parameters are set as default values. In the grid search model, the number of trees is 10 with 10 levels. 2 to 10 data samples are considered for splitting a node. Then the random grid is created using 5 fold cross-validation with 100 different combinations. For more tuning, a second-round random search is established for moderating the number of features by tuning the hyperparameters. Parameter selection, splitting the trees and selecting the samples for training the tree are described in the Grid Search Algorithm. In the RF classifier, parameter tuning is an essential factor for improving model performance. In the suggested method, six parameters such as n_estimators, Min-Leaf samples, Max-features, Max-depth, min-samp-split and bootstrap. Initially, the value n_estimators is set as 10. Min-Leaf samples portray the minimum number of samples at the end of the search. Its values are fixed as 1. A third and fourth hyperparameter is exploited to solve the overfitting of the training data. The tree min-samp-split parameter is tuned to regularize it. The last parameter, bootstrap, is set as the default value.

3.3. Validation Steps

All three models are evaluated using average accuracy and average errors, along with performance and compared to determine the best model's best parameters [86-92]. Generally, a random search narrows down the parameter ranges. Instead of sampling randomly, all the combinations of the parameters can be evaluated to determine the best parameters provided by the random search. If the performance decreases, then the hyper meter tuning is formulated. Features are selected corresponding to the hyperparameter tuning. Moreover, the feature importance is evaluated for obtaining model accuracy. In the proposed model, 7 features are deliberated to speed up the accuracy of the model. The steps of the Grid Search Algorithm are as follows:

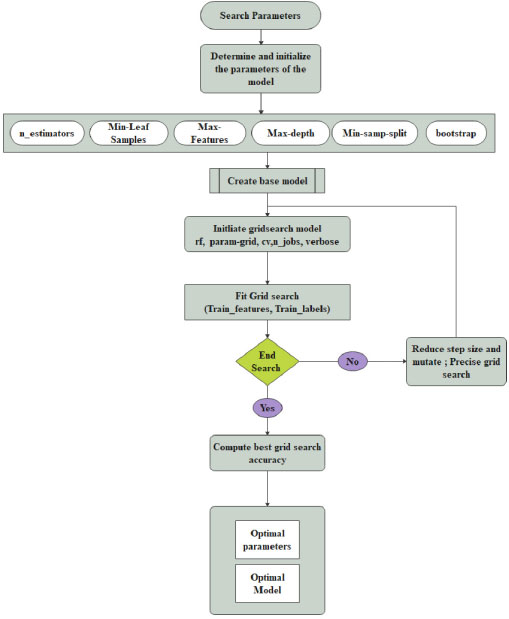
Fig. (2). Important feature selection from cleveland dataset.
Fig. (3). Data flow of grid search optimization.

3.4. Algorithm for Grid Search

Step 1: Initialize the params; n_estimators, M_features, M_depth, m_samsplit, m_samleaf, bootstrap

Step 2: Create a Parameter Grid

Step 3: Create a Base model (default model)

Step 4: Initiate Grid search model with params (rf, param-grid, cv, n_jobs, verbose)

Step 5: Find Grid Search with train_features, train_labels

Step 6: Compute the best grid.

Step 7: Print best param.

After evaluating the model, the data samples are examined for predicting the true positive (TPv), true negative (TNv), false positive (FPv) and False-negative (FNv). The propounded model addresses the Recall measure where the True positive rate is increased by reducing the false negatives. A recall is calculated as:

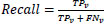(4)

Among the three models, the second grid model produces higher accuracy with a minimum error rate when compared to the other two models and produces higher recall results with the Random Forest classifier. The comparison of the Random classifier before and after grid search is obtained in Table 2. The heart disease dataset with 300 instances, correctly and incorrectly classified, is portrayed in the table, showing that grid optimization enhances RF classifier performance.

Among 300 instances, it is explicitly shown that 291 instances are correctly classified. The number of incorrect classifications is reduced after the grid search optimization by tuning n_estimators and min-samp-split, revealing that the Grid search model improves the performance of the RF classifier.

4. RESULTS AND EXPERIMENTS

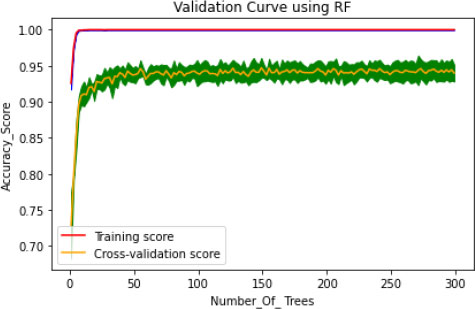
In the proposed model, the initial tree is set as 10, considering the performance of the model and its execution cost. 50 intervals increase the number of trees to speed up the performance of the model, such as 50, 100, 150, 200, 250 and 300. The train time varies for each set of trees, and it dramatically increases for every additional 50 number trees shown in Fig. (4). Simultaneously, the train time remains constant during the extraction of maximum features (Fig. 5). In this concern, it is essential to check for optimization values of the corresponding hyperparameters with a validation curve. Table 3 depicts the train time, validation score and training score for the number of trees. The validation scorestreaks at n=10 and starts fluctuating throughout the decision tree's entire traverse and explicate minimum variation from the training score. The hyperparameters such as n-estimators and min-samples –split are tuned to improve the performance of the Random Forest.

Table 2.
RF performance before and after grid search optimization.
No. of Instances Before Grid Search After Grid Search
Correctly Classified Incorrectly Classified Correctly Classified Incorrectly Classified
300 252 48 291 9
Fig. (4). Number of trees vs train time.
Fig. (5). Maximum features vs train time.
Fig. (6). Validation score with RF-grid search.
Table 3.
Performance score of RF with grid-search.
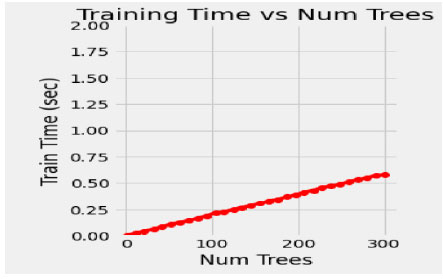
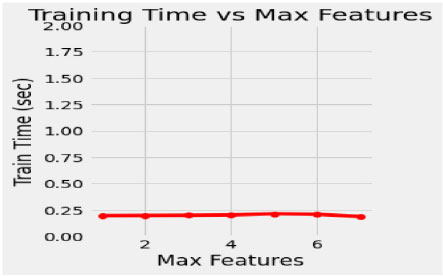
No. of Trees Train Time(Secs) Validation-Score Train-score
100 0.25 0.94 0.99
150 0.39 0.93 0.99
200 0.45 0.94 0.99
250 0.52 0.93 0.99
300 0.65 0.94 0.99

Generally, the model is optimized on training data to produce a better score, but on the other hand, if the model performs very well on the training set, it might provide poor results on a test set in some cases. This kind of overfitting paradigm can be solved by the cross-validation method. The hyperparameter optimization works well for overfitting only through the cv technique. Initially, the model fits k=5, training the four folds and finally evaluating the fifth fold. The model is trained on 1,2, 3 and 5th fold during the second turn, evaluating the fourth fold. This process is repeated 5 times, evaluating the new fold. At the end of every fold, the average performance is evaluated. The number of trees is trained in the proposed model, and accuracy of the cv score is probably nearer to the training score (Fig. 6). This validation is pursued to reduce the overfitting problem on the test data. The histogram plot of 14 attributes concerning the range values is presented in Fig. (7). To select the relevant features showing high correlation are selected and extracted using the grid search model. Thus seven features are chosen as essential features that increase the hyperparameters, such as n-estimators and min-samp-split. These features satisfy the classification performance in increasing the right positive rate.

Table 4 shows the performance measure of optimization models concerning the number of features extracted and several trees taken for the grid search method. The table shows the three models explored on data samples with 7 essential features for the optimization method. The first two models are carried with cross-validation and the second grid without cross-validation produces good results compared to the other two models.

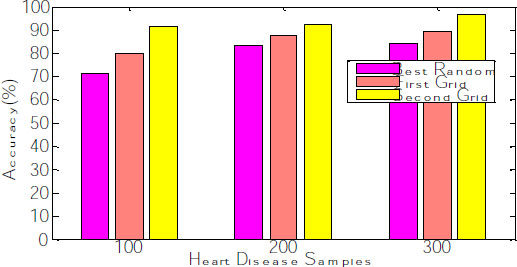
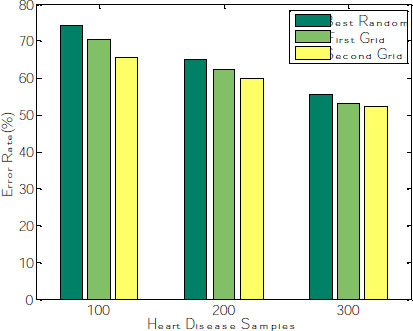
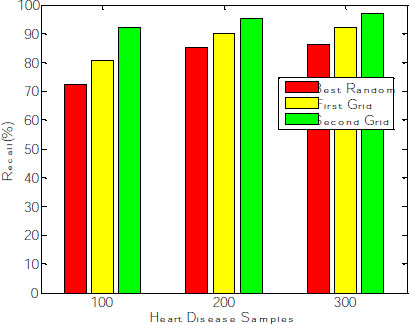
The corresponding graph concerning the accuracy, error rate and recall is shown in Fig. (8), exhibiting that the second grid model produces 91.34, 92.11 and 96.53 for 100, 200 and 300 samples. The other two models, such as best-random and First-grid, produce an average of 78% and 89%, which is less when compared to the third model.

Fig. (7). Feature ranges of heart disease dataset.
Table 4.
Performance measures of optimization models.
Optimization Models No. of Features No. of Trees Accuracy Error Rate Recall
Best-random 7 100 71.05 74.59 72.43
200 80.09 64.59 85.22
300 84.22 55.45 86.45
First-grid 7 100 90.03 70.19 80.98
200 87.59 62.43 90.26
300 89.44 53.32 92.17
Second-grid 7 100 91.34 65.45 92.12
200 92.11 60.44 95.25
300 96.53 52.17 97.01

After fitting the random model with 5 fold cross-validation by setting the random search, the parameters random grid, number of iterations= 100; cv= 5, verbose =2, random state= 42, the model need to be evaluated. Generally, the number of iterations needs to be reduced, leading to the over-fitting problem. Hyperparameter tuning is done on n_estimators and splitting the nodes at leaf level during the random search to alleviate this overfitting. The cross-validation curve can determine this. The mean absolute error (MAE) and Root means squared error(RMSE) decrease gradually when the number of trees is increased. The average error rate is evaluated and shown in Fig. (9). The graph explains that the Error rate is also reduced for the second grid compared with the other two models.

The proposed work contemplates increasing the positive rate and reducing the false-negative rate to identify patients with the disease for further treatment. Among 300 observations, 291 instances are correctly classified, wherein the recall rate of the proposed model increases concerning several samples. The best Random model produces an average recall rate of 81%. First-grid produces 87%, and Second Grid produces 95% of the sensitivity rate (Fig. 10), proving that the Random Forest classifier produces enhanced results after the Grid search optimization method deployed for feature extraction. The time complexity of the proposed model with Random Forest classifier is O(n*log(n)*d*k), where k=number of Decision Trees, n= number of training examples and d= number of dimensions of the data.

Fig. (8). Data samples vs accuracy.
Fig. (9). Data samples vs error rate.
Fig. (10). Data samples vs recall measure.

CONCLUSION

In this research, feature selection and feature extraction methods are based on the grid search optimization method. This method is used to select the feature, and the model is created and fit by tuning hyperparameters corresponding to the features and samples. The proposed model is designed by integrating the Random Forest (RF) classifier to determine relevant features. Grid Search Optimization (GSO) is applied to the heart disease dataset to predict disease, and the model is trained to increase the correct positive rate, thereby reducing the false negative. It increases the sensitivity measure of the Random Forest (RF) classifier. This grid search is integrated cross-validation to solve the over-fitting problem of the model. The proposed model selects essential features, and the model is trained on those features; thus, the dimensionality of samples is reduced to some extent.

Meanwhile, it increases the prediction accuracy of the RF model. Generally, random forest produces better accuracy in tuning the hyperparameter. The n-estimators and minimum split at the nodes are the two parameters tuned to enhance the performance of the model, which in turn increases RF classifier performance. When the model produces low accuracy, the model is created with another set of features. These combinations take some computational time to create another new model, which remains a challenge in the present work.

ETHICS APPROVAL AND CONSENT TO PARTICIPATE

Not applicable.

HUMAN AND ANIMAL RIGHTS

No animals/humans were used for studies that are the basis of this research.

CONSENT FOR PUBLICATION

Not applicable.

AVAILABILITY OF DATA AND MATERIALS

The heart disease dataset (Cleveland dataset) was collected from the UCI machine learning repository. The dataset consists of 14 features with 303 instances where 300 instances are taken for analysis.

FUNDING

None.

CONFLICT OF INTEREST

The authors declare no conflicts of interest, financial or otherwise.

ACKNOWLEDGEMENTS

Declared none.

REFERENCES

1
R. Spencer, F. Thabtah, N. Abdelhamid, and M. Thompson, "Exploring feature selection and classification methods for predicting heart disease", Digit. Health, vol. 6, 2020.
2
World Health Organization Cardiovascular Diseases, Available From: https://www.who.int/cardiovascular_diseases/en/ (accessed 9 June 2019).
3
A.K. Gárate-Escamila, A. Hajjam El Hassani, and E. Andrès, "Classification models for heart disease prediction using feature selection and PCA", Inform.Med. Unlocked, vol. 19, p. 100330, 2020.
4
S. Shalev-Shwartz, and S. Ben-David, Understanding machine learning: From theory to algorithms., Cambridge university press, 2014.
5
T. Hastie, R. Tibshirani, J.H. Friedman, and J.H. Friedman, The elements of statistical learning: data mining, inference, and prediction, vol. 2. Springer: New York, 2009, pp. 1-758.
6
M. Senekane, and B.M. Taele, "Prediction of solar irradiation using quantum support vector machine learning algorithm", Smart Grid Renew. Energy, vol. 7, no. 12, pp. 293-301, 2016.
7
Q. Ren, H. Cheng, and H. Han, Research on machine learning framework based on random forest algorithm.No. 1., vol. 1820. AIP Publishing LLC, 2017, p. 080020.AIP conference proceedings
8
I. Reis, D. Baron, and S. Shahaf, "Probabilistic random forest: A machine learning algorithm for noisy data sets", Astron. J., vol. 157, no. 1, p. 16, 2018.
9
A.H. Gonsalves, F. Thabtah, R.M.A. Mohammad, and G. Singh, "Prediction of coronary heart disease using machine learning: an experimental analysis", Proceedings of the 2019 3rd International Conference on Deep Learning Technologies, pp. 51-56, 2019.
10
F. Thabtah, "Machine learning in autistic spectrum disorder behavioral research: A review and ways forward", Inform. Health Soc. Care, vol. 44, no. 3, pp. 278-297, 2019.
11
M. Loog, Supervised classification: Quite a brief overview., Machine Learning Techniques for Space Weather, 2018, pp. 113-145.
12
F. Provost, C. Hibert, J.P. Malet, A. Stumpf, and C. Doubre, Automatic classification of endogenous seismic sources within a landslide body using random forest algorithm.EGU General Assembly Conference Abstracts, 2016.Vienna Austria
13
F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, and J. Vanderplas, "Scikit-learn: Machine learning in Python", J. Mach. Learn. Res, vol. 12, pp. 2825-2830, 2011.
14
M.S. Yang, and Y. Nataliani, "A feature-reduction fuzzy clustering algorithm based on feature-weighted entropy", IEEE Trans. Fuzzy Syst., vol. 26, no. 2, pp. 817-835, 2018.
15
M. Imani, and H. Ghassemian, "Feature extraction using weighted training samples", IEEE Geosci. Remote Sens. Lett., vol. 12, no. 7, pp. 1387-1391, 2015.
16
P. Wiesław, "Tree-based generational feature selection in medical applications", Procedia Comput. Sci., vol. 159, pp. 2172-2178, 2019.
17
B. Dun, E. Wang, and S. Majumder, "Heart disease diagnosis on medical data using ensemble learning", Comput. Sci., vol. 1, no. 1, pp. 1-5, 2016.
18
B.M. Asl, S.K. Setarehdan, and M. Mohebbi, "Support vector machine-based arrhythmia classification using reduced features of heart rate variability signal", Artif. Intell. Med., vol. 44, no. 1, pp. 51-64, 2008.
19
R. Ghawi, and J. Pfeffer, "Efficient hyperparameter tuning with grid search for text categorization using kNN approach with BM25 similarity", Open Comput. Sci., vol. 9, no. 1, pp. 160-180, 2019.
20
K. Vembandasamy, R. Sasipriya, and E. Deepa, "Heart diseases detection using Naive Bayes algorithm. International Journal of Innovative Science", Eng. Tech., vol. 2, no. 9, pp. 441-444, 2015.
21
A. Malav, K. Kadam, and P. Kamat, "Prediction of heart disease using K-means and artificial neural network as hybrid approach to improve accuracy", IACSIT Int. J. Eng. Technol., vol. 9, no. 4, pp. 3081-3085, 2017.
22
A.H. Victoria, and G. Maragatham, "Automatic tuning of hyperparameters using Bayesian optimization", Evol. Syst., vol. 12, no. 1, pp. 217-223, 2021.
23
S. Geeitha, and M. Thangamani, "Incorporating EBO-HSIC with SVM for gene selection associated with cervical cancer classification", J. Med. Syst., vol. 42, no. 11, p. 225, 2018.
24
E.K. Hashi, and M.S.U. Zaman, Md. Shahid Uz Zaman, "Developing a hyperparameter tuning based machine learning approach of heart disease prediction", J. Appl. Sci. Proc. Eng., vol. 7, no. 2, pp. 631-647, 2020.
25
P. Motarwar, A. Duraphe, G. Suganya, and M. Premalatha, "Cognitive approach for heart disease prediction using machine learning", 2020 International Conference on Emerging Trends in Information Technology and Engineering (ic-ETITE), pp. 1-5, 2020.
26
J. Jayashree, J. Vijayashree, V. Goar, and N.C.S. Iyengar, "Artificial neural networks with enhanced nearest neighbor algorithm for heart disease prediction", High Technol. Lett., vol. 26, no. 9, 2020.
27
M.M.A. Rahhal, Y. Bazi, H. AlHichri, N. Alajlan, F. Melgani, and R.R. Yager, "Deep learning approach for active classification of electrocardiogram signals", Inf. Sci., vol. 345, pp. 340-354, 2016.
28
G. Guidi, M.C. Pettenati, P. Melillo, and E. Iadanza, "A machine learning system to improve heart failure patient assistance", IEEE J. Biomed. Health Inform., vol. 18, no. 6, pp. 1750-1756, 2014.
29
G. Parthiban, and S.K. Srivatsa, "Applying machine learning methods in diagnosing heart disease for diabetic patients", Int. J. Appl. Inf. Syst., vol. 3, no. 7, pp. 25-30, 2012.
30
R.S. Singh, B.S. Saini, and R.K. Sunkaria, "Detection of coronary artery disease by reduced features and extreme learning machine", Clujul Med., vol. 91, no. 2, pp. 166-175, 2018.
31
R. Rajagopal, and V. Ranganathan, "Evaluation of effect of unsupervised dimensionality reduction techniques on automated arrhythmia classification", Biomed. Signal Process. Control, vol. 34, pp. 1-8, 2017.
35
S. Mohan, C. Thirumalai, and G. Srivastava, "Effective heart disease prediction using hybrid machine learning techniques", IEEE Access, vol. 7, pp. 81542-81554, 2019.
36
V.V. Ramalingam, A. Dandapath, and M.K. Raja, "Heart disease prediction using machine learning techniques: A survey", Int J. Eng. Techn., vol. 7, no. 2.8, pp. 684-687, 2018.
37
A. Rajdhan, A. Agarwal, M. Sai, D. Ravi, and P. Ghuli, "Heart disease prediction using machine learning", Int. J. Res. Technol, vol. 9, no. 04, pp. 659-662, 2020.
38
D. Shah, S. Patel, and S.K. Bharti, "Heart disease prediction using machine learning techniques", SN Computer Science, vol. 1, no. 6, p. 345, 2020.
39
D.N. Silva, L.D. Pacifico, and T.B. Ludermir, "An evolutionary extreme learning machine based on group search optimization", 2011 IEEE Congress of Evolutionary Computation (CEC), pp. 574-580, 2011.
40
J. Patel, "Heart disease prediction using machine learning and data mining technique", Heart Dis., vol. 7, no. 1, pp. 129-137, 2015.
41
Y. Khourdifi, and M. Bahaj, "Heart disease prediction and classification using machine learning algorithms optimized by particle swarm optimization and ant colony optimization", Int. J. Intell. Eng. Syst., vol. 12, no. 1, pp. 242-252, 2019.
42
A.K. Dwivedi, "Performance evaluation of different machine learning techniques for prediction of heart disease", Neural Comput. Appl., vol. 29, no. 10, pp. 685-693, 2018.
43
N. Bhatla, and K. Jyoti, "An analysis of heart disease prediction using different data mining techniques", Int. J. Eng., vol. 1, no. 8, pp. 1-4, 2012.
44
P. Probst, A.L. Boulesteix, and B. Bischl, "Tunability: Importance of hyperparameters of machine learning algorithms", J. Mach. Learn. Res., vol. 20, no. 1, pp. 1934-1965, 2019.
45
A. Methaila, P. Kansal, H. Arya, and P. Kumar, "Early heart disease prediction using data mining techniques", Comp. Sci. Inform. Technol. J., vol. 28, pp. 53-59, 2014.
46
I. Syarif, A. Prugel-Bennett, and G. Wills, "SVM parameter optimization using grid search and genetic algorithm to improve classification performance", Telkomnika (Telecommunication Computing Electronics and Control), vol. 14, no. 4, pp. 1502-1509, 2016.
47
P. Liashchynskyi, and P. Liashchynskyi, "Grid search, random search, genetic algorithm: a big comparison for NAS", arXiv, 2019.
48
J. Bergstra, and Y. Bengio, "Random search for hyper-parameter optimization", J. Mach. Learn. Res., vol. 13, no. 2, 2012.
49
J. Snoek, H. Larochelle, and R.P. Adams, "Practical bayesian optimization of machine learning algorithms", Adv. Neural Inf. Process. Syst., p. 25, 2012.
50
F.J. Pontes, G.F. Amorim, P.P. Balestrassi, A.P. Paiva, and J.R. Ferreira, "Design of experiments and focused grid search for neural network parameter optimization", Neurocomputing, vol. 186, pp. 22-34, 2016.
51
M. Reif, F. Shafait, and A. Dengel, "Meta-learning for evolutionary parameter optimization of classifiers", Mach. Learn., vol. 87, no. 3, pp. 357-380, 2012.
52
A.A. Akinyelu, and A.O. Adewumi, "Classification of phishing email using random forest machine learning technique", J. Appl. Math., vol. 2014, pp. 1-6, 2014.
53
V. Rodriguez-Galiano, M. Sanchez-Castillo, M. Chica-Olmo, and M. Chica-Rivas, "Machine learning predictive models for mineral prospectivity: An evaluation of neural networks, random forest, regression trees and support vector machines", Ore Geol. Rev., vol. 71, pp. 804-818, 2015.
54
D. Wu, C. Jennings, J. Terpenny, R.X. Gao, and S. Kumara, "A comparative study on machine learning algorithms for smart manufacturing: tool wear prediction using random forests", J. Manuf. Sci. Eng., vol. 139, no. 7, p. 071018, 2017.
55
I. Ahmad, M. Basheri, M.J. Iqbal, and A. Rahim, "Performance comparison of support vector machine, random forest, and extreme learning machine for intrusion detection", IEEE Access, vol. 6, pp. 33789-33795, 2018.
56
S.A. Naghibi, H.R. Pourghasemi, and B. Dixon, "GIS-based groundwater potential mapping using boosted regression tree, classification and regression tree, and random forest machine learning models in Iran", Environ. Monit. Assess., vol. 188, no. 1, p. 44, 2016.
57
R. Bardenet, M. Brendel, B. Kégl, and M. Sebag, "Collaborative hyperparameter tuning", Int. Conf. Mach Learn, pp. 199-207, 2013.
58
J. Li, K. Cheng, S. Wang, F. Morstatter, R.P. Trevino, J. Tang, and H. Liu, "Feature Selection", ACM Comput. Surv., vol. 50, no. 6, pp. 1-45, 2018.
59
K. Kira, and L.A. Rendell, A practical approach to feature selection.Mach. learn. Proceed 1992., Morgan Kaufmann, 1992, pp. 249-256.
60
G. Chandrashekar, and F. Sahin, "A survey on feature selection methods", Comput. Electr. Eng., vol. 40, no. 1, pp. 16-28, 2014.
61
Y. Saeys, I. Inza, and P. Larranaga, "A review of feature selection techniques in bioinformatics", Bioinformatics, vol. 23, no. 19, pp. 2507-2517, 2007.
62
M. Dash, and H. Liu, "Feature selection for classification", Intell. Data Anal., vol. 1, no. 1-4, pp. 131-156, 1997.
63
J. Cai, J. Luo, S. Wang, and S. Yang, "Feature selection in machine learning: A new perspective", Neurocomputing, vol. 300, pp. 70-79, 2018.
64
K. Kira, and L.A. Rendell, "The Feature Selection Problem: Traditional Methods and a New Algorithm", AAAI Conference on Artificial Intelligence, vol. 2, pp. 129-134, 1992.
65
Y. Saeys, T. Abeel, and Y.V.D. Peer, "Robust feature selection using ensemble feature selection techniques", Joint European conference on Machine Learning and Knowledge Discovery in Databases, pp. 313-325, 2008.Berlin, Heidelberg
66
P. Mitra, C.A. Murthy, and S.K. Pal, "Unsupervised feature selection using feature similarity", IEEE Trans. Pattern Anal. Mach. Intell., vol. 24, no. 3, pp. 301-312, 2002.
67
P. Agrawal, H.F. Abutarboush, T. Ganesh, and A.W. Mohamed, "Metaheuristic algorithms on feature selection: A survey of one decade of research (2009-2019)", IEEE Access, vol. 9, pp. 26766-26791, 2021.
68
S.W. Lin, K.C. Ying, S.C. Chen, and Z.J. Lee, "Particle swarm optimization for parameter determination and feature selection of support vector machines", Expert Syst. Appl., vol. 35, no. 4, pp. 1817-1824, 2008.
69
A. Javeed, S. Zhou, L. Yongjian, I. Qasim, A. Noor, and R. Nour, "An intelligent learning system based on random search algorithm and optimized random forest model for improved heart disease detection", IEEE Access, vol. 7, pp. 180235-180243, 2019.
70
D. Tomar, and S. Agarwal, "Feature selection based least square twin support vector machine for diagnosis of heart disease", Int. J. Bio-Sci Bio-Technol, vol. 6, no. 2, pp. 69-82, 2014.
71
A. Javeed, S.S. Rizvi, S. Zhou, R. Riaz, S.U. Khan, and S.J. Kwon, "Heart risk failure prediction using a novel feature selection method for feature refinement and neural network for classification", Mob. Inf. Syst., vol. 2020, pp. 1-11, 2020.
72
H. Ahmed, E.M.G. Younis, A. Hendawi, and A.A. Ali, "Heart disease identification from patients’ social posts, machine learning solution on Spark", Future Gener. Comput. Syst., vol. 111, pp. 714-722, 2020.
73
B.A. Tama, S. Im, and S. Lee, "Improving an intelligent detection system for coronary heart disease using a two-tier classifier ensemble", BioMed Res. Int., vol. 2020, pp. 1-10, 2020.
74
S. Iftikhar, K. Fatima, A. Rehman, A.S. Almazyad, and T. Saba, "An evolution based hybrid approach for heart diseases classification and associated risk factors identification", Biomed. Res., vol. 28, no. 8, pp. 3451-3455, 2017.
75
Z. Zhang, J. Dong, X. Luo, K.S. Choi, and X. Wu, "Heartbeat classification using disease-specific feature selection", Comput. Biol. Med., vol. 46, pp. 79-89, 2014.
76
R. Bharti, A. Khamparia, M. Shabaz, G. Dhiman, S. Pande, and P. Singh, "Prediction of heart disease using a combination of machine learning and deep learning", Comput. Intell. Neurosci., vol. 2021, pp. 1-11, 2021.
77
M. Tubishat, N. Idris, L. Shuib, M.A.M. Abushariah, and S. Mirjalili, "Improved Salp Swarm Algorithm based on opposition based learning and novel local search algorithm for feature selection", Expert Syst. Appl., vol. 145, p. 113122, 2020.
78
M.N. Akhter, S. Mekhilef, H. Mokhlis, and N. Mohamed Shah, "Review on forecasting of photovoltaic power generation based on machine learning and metaheuristic techniques", IET Renew. Power Gener., vol. 13, no. 7, pp. 1009-1023, 2019.
79
L. Ali, A. Niamat, J.A. Khan, N.A. Golilarz, X. Xingzhong, A. Noor, R. Nour, and S.A.C. Bukhari, "An optimized stacked support vector machines based expert system for the effective prediction of heart failure", IEEE Access, vol. 7, pp. 54007-54014, 2019.
80
B. Abdollahzadeh, and F.S. Gharehchopogh, "A multi-objective optimization algorithm for feature selection problems", Eng. Comput., vol. 38, no. S3, pp. 1845-1863, 2022.
81
S. Prabu, B. Thiyaneswaran, M. Sujatha, C. Nalini, and S. Rajkumar, "Grid Search for Predicting Coronary Heart Disease by Tuning Hyper-Parameters", Comput. Syst. Sci. Eng., vol. 43, no. 2, pp. 737-749, 2022.
82
I.M. El-Hasnony, O.M. Elzeki, A. Alshehri, and H. Salem, "Multi-label active learning-based machine learning model for heart disease prediction", Sensors (Basel), vol. 22, no. 3, p. 1184, 2022.
83
P. Rani, R. Kumar, N.M.O.S. Ahmed, and A. Jain, "A decision support system for heart disease prediction based upon machine learning", J. Reliab. Intell. Environ., vol. 7, no. 3, pp. 263-275, 2021.
84
M.M. Ahsan, and Z. Siddique, "Machine learning-based heart disease diagnosis: A systematic literature review", Artif. Intell. Med., vol. 128, p. 102289, 2022.
85
G.Y.H. Lip, A. Genaidy, G. Tran, P. Marroquin, C. Estes, and S. Sloop, "Improving stroke risk prediction in the general population: a comparative assessment of common clinical rules, a new multimorbid index, and machine-learning-based algorithms", Thromb. Haemost., vol. 122, no. 1, pp. 142-150, 2022.
86
A. Al-Fugara, M. Ahmadlou, A.R. Al-Shabeeb, S. AlAyyash, H. Al-Amoush, and R. Al-Adamat, "Spatial mapping of groundwater springs potentiality using grid search-based and genetic algorithm-based support vector regression", Geocarto Int., vol. 37, no. 1, pp. 284-303, 2022.
87
V.R.E. Christo, H.K. Nehemiah, J. Brighty, and A. Kannan, "Feature selection and instance selection from clinical datasets using co-operative co-evolution and classification using random forest", J. Inst. Electron. Telecommun. Eng., vol. 68, no. 4, pp. 2508-2521, 2022.
88
N. Mahendran, and D.R.V. P M, "A deep learning framework with an embedded-based feature selection approach for the early detection of the Alzheimer’s disease", Comput. Biol. Med., vol. 141, p. 105056, 2022.
89
R.A. Disha, and S. Waheed, "Performance analysis of machine learning models for intrusion detection system using Gini Impurity-based Weighted Random Forest (GIWRF) feature selection technique", Cybersecurity, vol. 5, no. 1, pp. 1-22, 2022.
90
G. Saranya, and A. Pravin, "A novel feature selection approach with integrated feature sensitivity and feature correlation for improved prediction of heart disease", J. Ambient Intell. Humaniz. Comput., pp. 1-15, 2022.
91
G. Saranya, and A. Pravin, "Hybrid global sensitivity analysis based optimal attribute selection using classification techniques by machine learning algorithm", Wirel. Pers. Commun., pp. 1-20, 2021.
92
A. Abdellatif, H. Abdellatef, J. Kanesan, C.O. Chow, J.H. Chuah, and H.M. Gheni, "Improving the heart disease detection and patients’ survival using supervised infinite feature selection and improved weighted random forest", IEEE Access, vol. 10, pp. 67363-67372, 2022.