All published articles of this journal are available on ScienceDirect.
Simulation of Bronchial Airflow in COPD Patients
Abstract
Aim:
This research tackles the problem of assessing airflow inside both a healthy and a COPD bronchus ramification, by a Finite Element Method (FEM) computational mode.
Background:
Chronic Obstructive Pulmonary Disease (COPD) is considered the third leading cause of death worldwide, smoking being the most common risk factor. In the case of emphysema, the appearance of bullae in the upper and middle lobes is frequent.
Objective:
Bullae tend to increase their size progressively with time, severely clogging bronchi. In this research, bullae with different sizes are modelled as semi-spheres located at the internal wall of a 3D tomographic-based bronchi model.
Methods:
Several numerical analyses were performed by applying fluid interaction focused on the behaviour of flow through a fifth generations bronchus bifurcation in different cases and degrees of the advance of COPD.
Results:
The outcome provides the gradients of flow speed and pressure within the bronchus ramification in the considered cases.
Conclusion:
The methodology herein proposed is applicable to determine the airflow within any patient’s bronchus bifurcation were bullae appear, and thereby to assess and improve the design of custom treatments.
1. INTRODUCTION
Chronic obstructive pulmonary disease (COPD) is a significant cause of morbidity, and it is the third leading cause of death worldwide [1]. COPD is characterized by “expiratory airflow limitation that is not fully reversible, deregulated chronic inflammation, and emphysematous destruction of the lungs” [2]. While research suggests that elderly people are more vulnerable to COPD [3], in the case of suffering emphysema, it is characterized by a bronchial obstruction and destruction of lung parenchyma [4-6]. Lung emphysema generates internal bullae that are usually located in the upper and middle lobes. Bullae are spaces of natural forms (round, oval or elongated) that increase their size progressively over time, being reported up to 12.7 x 10.1 cm2 in the middle lobe (giant bullae) [7]. It is clearly of great importance to deeply comprehend the dynamical behaviour of airflow through bronchial ramifications affected by COPD as the disease advances. In current literature, authors focus on the study of flow rates and Reynolds numbers of flow passage through healthy bronchi. For instance, Balásházy [8] found that, fourth and fifth bronchus ramification generations are characterized by flow rates of 7.5 L/s, while Y Liu [9] proposed that in fifth, sixth and seventh bronchi ramification generations, the flow regime occurs at Reynolds numbers between 200 and 1600, and flow rates between 0.27 to 2.16 L/s. Freitas [10] performed simulations of bronchial flow with a Reynolds number of 1250, while Piglione [11] assessed properties of flow in moderate activity condition for bronchial generations fourth to fifteen. Nemes [12] presented Reynolds stress patterns due to turbulence even at the first bronchial bifurcation. Nonetheless, very little research has been performed in the assessment of airflow through obstructed bronchi, particularly by bullae. This research tackles the problem of assessing airflow inside both a healthy and a COPD bronchus ramification, by a Finite Element Method (FEM) computational model. FEM has been successfully applied to a wide range of applications within science, and for the determination of biological flow behaviours [13-15]. In order to perform flow-based FEM analyses, the bronchial bifurcation model was generated through several continuous tomographic slices to keep it as realistic as possible. In Section 2, the 3D model of bronchi was generated, and the boundary conditions of numerical studies were set. In Section 3, we present three study cases of bronchial airflow as follows: within a healthy bronchus, within a bronchus with a growing bulla and within a bronchus with two bullae. Finally, in Section 4, we present a discussion and some final remarks.
2. MATERIALS AND METHODS
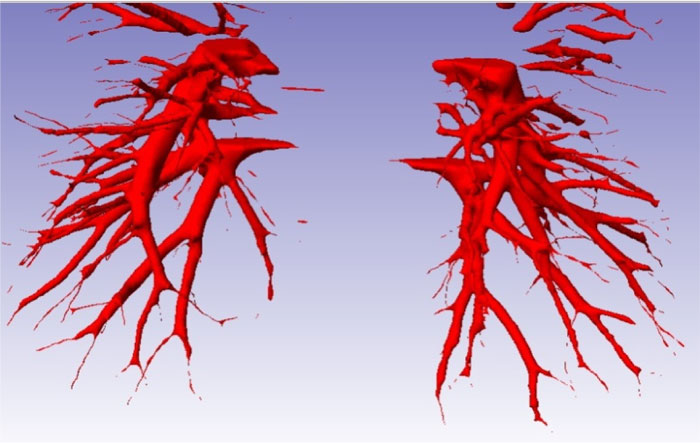
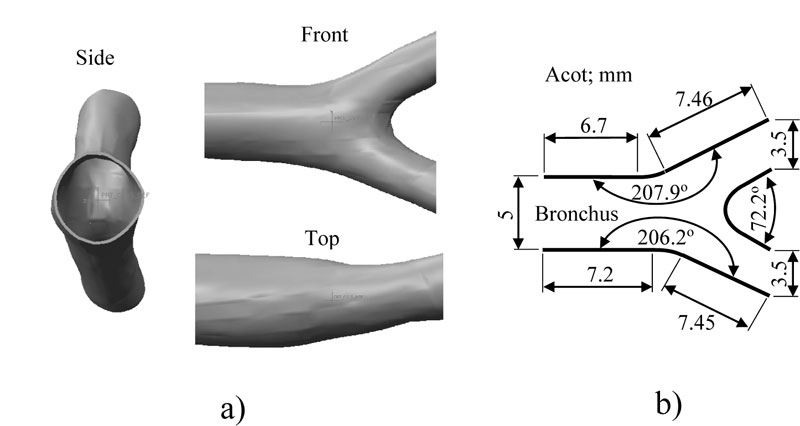
The main limitation to design the bronchi model is the intricate bronchi ramification geometry. To overcome this problem, 270 topographic slices of the thorax were taken from Mexican male adult around 32 years old to obtain a precise model of pulmonary bronchi. The model is asymmetric with significant irregularities. The definition of the numerical model was based on the bronchial system surface, where software was applied to draw blocks of surfaces that cover all the areas around the geometry of the bronchus (Fig. 1). The model discontinuities at the surface junctions were filled with a SCAN IP® computer program for all gaps to be closed and geometry errors corrected; also, a thickness of 0.005 mm (that is approximately the thickness of the real tissue) was added (Fig. 2a). The bronchus model was then discretized with a low order element with flow capacities. The flow and structural numerical simulations were performed using Finite Element Method (FEM) software, ANSYS® student version.
2.1. FEM Boundary Conditions
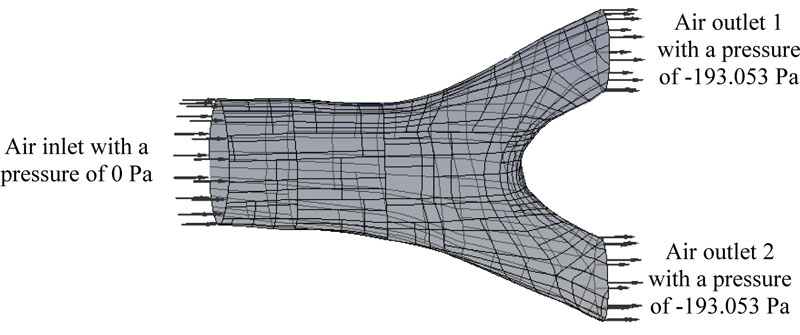
The bronchial system is considered to work as a pipe boundary condition where the air will flow. The pressure inside the lung was set around to -193.053 Pa being the atmospheric pressure set to 0 Pa, which is an average respiratory data (Fig. 3). The considered average cross-section of the bronchus is 19.600 mm2, for an average bronchus diameter of 5 mm (Fig. 2b) and a volumetric flow speed of 2.160 x 10-3 m3/s [16]. Accordingly, the average flow velocity was contemplated as s = 7.649 m/s. The air properties at a temperature of 37 oC, density of 1225 kg/m3 and dynamic viscosity of 1.789 x 10-5 Pa-s (Pascal-second) were taken into consideration. These values were substituted into Reynolds number equation [17] and if the greatest diameter for the bronchus is 4.5 mm, then Ns = 2744.490. Consequently, the initial values were defined, taking the 3D bronchus model to represent the inputs and outputs of the air. In Fig. (3), the initial flow conditions to carry out the numerical analysis are shown. Where the output pressure is less than the inlet pressure, this pressure difference allows air to be directed to the alveolus.
3. RESULTS
The analyzed bronchial system consists of bifurcation from a 5th to 6th generation of bronchial ramifications. There is a common zone where bullae tend to grow in COPD patients. Moreover, a geometric representation of the bronchus bifurcation with general dimensions is presented in Fig. (2b).
3.1. The First Case of Study
The numerical study of a healthy bronchus was carried out in order to obtain the initial and optimal flow velocity and pressure working values for the system. These values could be used as comparative parameters for the study cases. The numerical simulation of flow through the healthy bronchus was conducted by applying FEM algorithms. The initial air conditions were defined (Fig. 3), and the solution of the system converged after around 100 iterations.
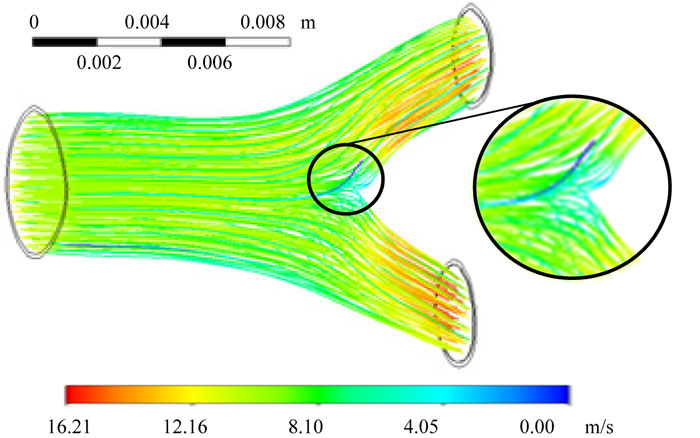
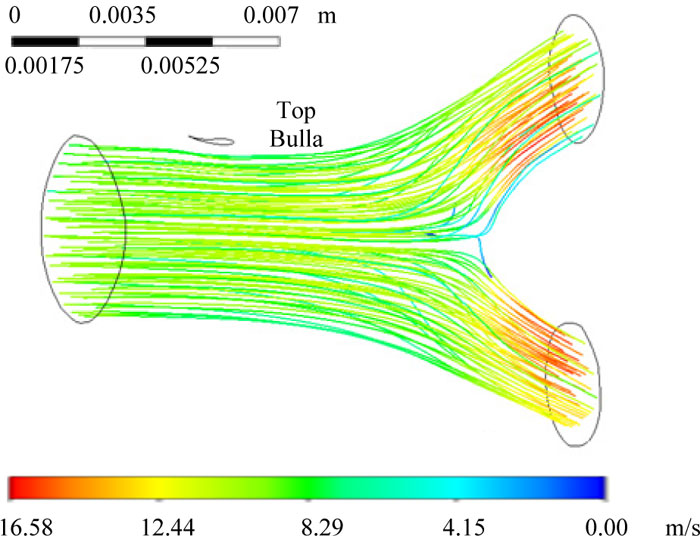
The numerical simulation revealed that the rate at which air moved within the bronchial ramifications was between 0 to 16.216 m/s, with a Reynolds number of Ns =2744.49. The lowest value in the airspeed was generated by a pressure gradient located in the bifurcation, where the fluid impacts at the bronchial carina (Fig. 4). FEM analysis also provided the inlet and outlet mass balance relations due to the bifurcation that for the air output 2, there was a higher flow due to the bronchial ramification geometry and the pressure gradient generated at the bifurcation (Table 1, Fig. 4).
3.2. The Second Case of Study
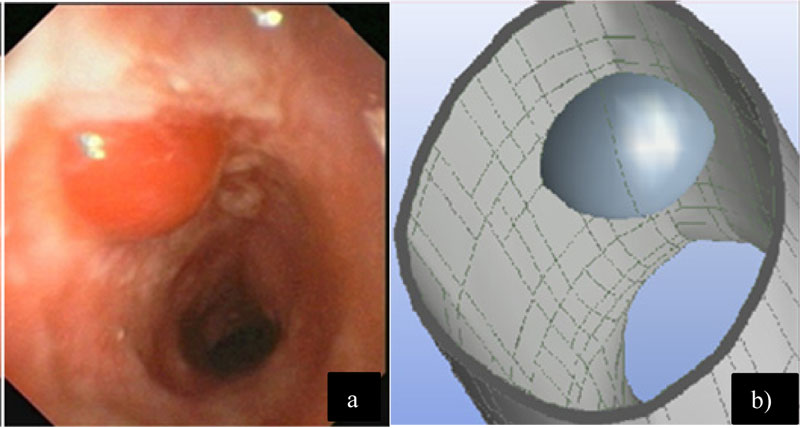
In this case, the airflow with the introduction of a bulla located at the bronchial ramification is studied. In Fig. (5a), a bulla inside the bronchus that was produced by lung emphysema is shown. In Fig. (5b), a semi-spherical geometry was added into the bronchial ramification model in order to perform the numerical analysis assessment of the bulla effect [18].
| Data | Mass balance (kg/s) |
|---|---|
| Maximum speed (m/s) | 16.216 |
| Inlet | 0.101 |
| Outlet 1 | -0.049 |
| Outlet 2 | -0.051 |
| Loss | 1.519 x 10-5. |
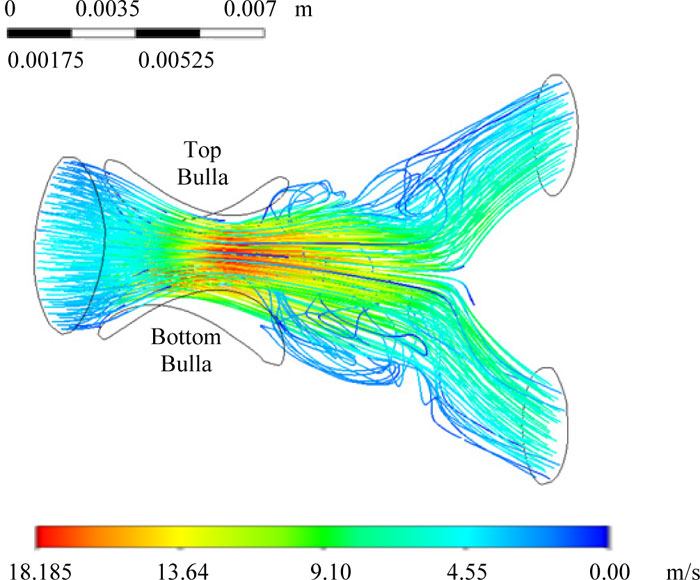
Initially, the bulla was considered with a diameter of 1.25 mm and located (Fig. 6) at the top surface of the singular bifurcation of the bronchus. In Fig. (6), the numerical results for the air rate and flow movement inside the bronchus ramification are shown. The flow rate was in the range from 0 to 16.584 m/s (Fig. 6). As seen in the previous case, the lowest value of airspeed was located by a pressure gradient, which is generated at the bifurcation (Fig. 6). In Table 2, the mass balance produced by the airspeed by a single bulla of 1.25 mm diameter was featured.
Furthermore, in order to assess the growing process of a bulla, a variation on its size can be produced to perform different numerical analyses of its effect on the flow. The analyses were performed considering the same parameters of the two later cases, but with respective bulla sizes of 2.5 mm, 3.75 mm and 5 mm diameter, respectively. Table 3 presents the mass balance produced by bulla growth.
| Data | Mass balance (kg/s) |
|---|---|
| Maximum speed (m/s) | 16.584 |
| Inlet | 19.062 x 10 -5 |
| Outlet 1 | -9.148 x 10 -5 |
| Outlet 2 | -9.914 x 10-5 |
| Loss | 4.51 x 10-5 |
| Data | Mass balance (kg/s) | ||
|---|---|---|---|
| Bulla diameter size (mm) | |||
| 2.5 | 3.75 | 5 | |
| Maximum speed (m/s) | 15.737 | 16.136 | 16.361 |
| Inlet | 18.636 x 10-5 | 18.339 x 10-5 | 18.698 x 10-5 |
| Outlet 1 | -9.002 x 10-5 | -8.855 x 10-5 | -8.966 x 10-5 |
| Outlet 2 | -9.635 x 10-5 | -9.487 x 10-5 | -9.736 x 10-5 |
| Loss | -1.653 x 10-8 | -9.487 x 10-5 | -5.308 x 10-5 |
| Data | Mass balance (kg/s) | |||
|---|---|---|---|---|
| Bulla diameter size (mm) | ||||
| 1.25 | 2.5 | 3.75 | 5 | |
| Maximum speed (m/s) | 15.611 | 17.418 | 21.644 | 18.185 |
| Inlet | 16.851 x 10-5 | 15.734 x 10-5 | 15.001 x 10-5 | 7.292 x 10-5 |
| Outlet 1 | -8.213 x 10-5 | -7.719 x 10-5 | -7.265 x 10-5 | -3.412 x 10-5 |
| Outlet 2 | -8.649 x 10-5 | --8.030 x 10-5 | -7.753 x 10-5 | -3.885 x 10-5 |
| Loss | -0.010 x 10-5 | -0.016 x 10-7 | -0.017 x 10-5 | -6.223 x 10-5 |
3.3. Third Case of Study
This case considers the numerical simulations of two bullae within the bronchial ramification. The first bulla was located at the top of the bronchus, with a constant diameter of 5 mm. A second bulla was located at the bottom surface of the bronchus, at 180° from the top bulla. The latter is growing as a result of pulmonary emphysema, affecting the air inflow into the bronchus and decreasing pressure and speed. The growing bulla initial diameter size was 1.25 mm for a first analysis, and subsequently, it was increased to 2.5 mm, 3.75 mm, and 5 mm. The results from these simulations are shown in Table 4.
Numerical Mass balance study determines the degree of damage generated by bullae located in airways. From these data, the constriction of the airflow was clearly observed when a second bulla grew to simulate advanced cases of COPD patients. Fig. (7) presents the numerical results for the critical case of massive bullae obstruction, where the bronchus had two bullae of 5 mm diameter each at the top and bottom surfaces.
Fig. (8) summarizes the data obtained from the numerical simulation of Case B (a single bulla) and the numerical simulation of Case C (double bullae). It is shown on the left side the velocity scale, and on the right side, it is shown the air mass outlet flow loss at the end of the bronchi. Case B is shown in yellow. Case C is shown in green. The velocity measured with no bullae is shown in grey only for visual reference. By comparing Case B velocity versus velocity with no bullae, only 2% of the variation is presented. Thus, this variation has a direct relation with the air mass flow loss at the outlet ends of the bronchi. The measured values of this section have a constant drop directly correlated with the increased size of the bullae. On the other hand, the values shown for Case C had similar behaviour until the third change in the size of the bullae. On this numerical simulation, the boundary conditions cause an increase of 37% of the velocity against the initial
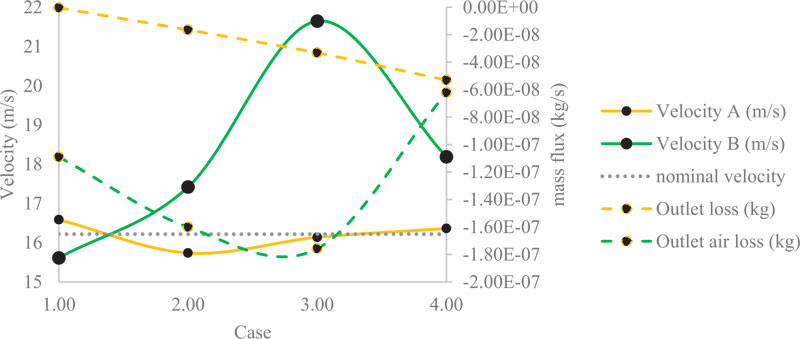
velocity measured on the numerical simulation with no bullae. This change has consequences because it decreases the drop of the air mass flow loss at the outlet end of the bronchi. This change can be attributable to the vortex effect with a considerable size of the bullies. Bronchi cross-section remains constant along with the bullies and the carina, decreasing the velocity of the air but catching more air on this space during the process of breathing. The vorticity and the pressure could be affected by the vortex effect.
4. DISCUSSION
Patients with Chronic Obstructive Pulmonary Disease (COPD) present breathing complications, which depend on the progress of the disease as well as of the properties of bullae developing at bronchi (obstructing of airflow). In this paper, the flow-structural numerical simulation of flow behaviour through both a healthy and a bronchus with pulmonary emphysema (one bulla, two bullae and variations in the diameters of bullae) was performed. To be able to perform the numerical analyses accurately, a fifth-generation bronchi 3D model was obtained by a series of tomographic slices. In general, diseases tend to modify the biological and physical characteristics of the patient’s processes dynamically. Thus, numerical simulations are not entirely accurate, due to the constant modification of biological factors that evolve, which are strictly related to the specific disease as well as to the patient itself. Hence, there were some essential simplifications made in order to be able to perform the numerical analyses as presented. The bullae geometry was approximated by a spherical shape, and that some biophysical factors as the mucous membrane and structural integrity of the bronchus, were not considered due to FEM software limitations. Nevertheless, the results obtained in this paper showed a positive correlation with the ones reported in the literature [9, 11].
CONCLUSION
Regarding the numerical results obtained for flow rates within the bronchus of 5-9 m/s, they were found to be consistent with those reported by Liu [9]. The differences between the results are probably explained by the bronchus geometry model considered in each work. In addition, it is observed that small changes in very small scales yield to important modifications in the mechanical properties of materials and can drastically modify the numerical results. On the other side, the results of airflow within the healthy bronchus (first case of study) are on agreement with those by Piglione [11], which considered a lower flow regime and a smaller bronchus model than the ones herein considered. With respect to the modelling of bullae, although a more realistic model of bullae could be generated by tomographic slices of a bronchus featuring them, in this research, they were modelled as semi-spheres to both simplify the problem and provide new knowledge on how the respiratory system behaves on generic realistic cases. Of course, for a specific patient, the best results would be yielded by a tomographic-based model of bullae. The bronchial bifurcation used to perform the numerical simulations is only one of the many that constitute the respiratory system (both in sign and slope). Although it was selected at a generation of bronchial ramifications where bullae are more common to appear, the methodology herein proposed was applicable to determine the airflow within any patient’s bronchus bifurcation where bullae appear, and thereby to assess and improve the design of custom treatments.
ETHICS APPROVAL AND CONSENT TO PARTICIPATE
Not applicable.
HUMAN AND ANIMAL RIGHTS
Not applicable.
CONSENT FOR PUBLICATION
Not applicable.
AVAILABILITY OF DATA AND MATERIALS
The data used to support the findings of this study are available from the corresponding author [C.R] upon request.
FUNDING
The study is financially supported by the Mexican government by the Consejo Nacional de Ciencia y Tecnología. Authors acknowledge partial support projects 20201964 and 20200930, as well as EDI grant, all provided by SIP/IPN.
CONFLICT OF INTEREST
The authors declare that they have no conflict of interest.
ACKNOWLEDGEMENTS
The authors gratefully acknowledge the financial support from the Mexican government by the Consejo Nacional de Ciencia y Tecnología. Authors acknowledge partial support projects as well as EDI grant, all provided by SIP/IPN.


