RESEARCH ARTICLE


Entropy Measures with Three-axis Motion Time-series Data: Comparison of Dominant and Non-dominant Hand in Multi-directional Reach



Nuttaporn Praditpod1, 2, Phongpan Tantipoon2, Xinyu Zhang3, Petra Rauchhaus4, Chunhui Li1, *, Zhihong Huang1
1 Department of Biomedical Engineering, School of Science and Engineering, University of Dundee, Dundee, United Kingdom
2 Department of Physical Therapy, Faculty of Allied Health Sciences, Thammasat University, Bangkok, Thailand
3 School of Medicine, University of Dundee, Dundee, United Kingdom
4 Tayside Clinical Trials Unit (TCTU), School of Medicine, University of Dundee, Dundee, United Kingdom

Article Information


Identifiers and Pagination:

Year: 2023
Volume: 17
E-location ID: e187412072304100
Publisher ID: e187412072304100
DOI: 10.2174/18741207-v17-e230420-2022-22

Article History:

Received Date: 05/10/2022
Revision Received Date: 13/03/2023
Acceptance Date: 15/03/2023
Electronic publication date: 23/06/2023
Collection year: 2023

Article Metrics

CrossRef Citations:
0
Total Statistics:

Full-Text HTML Views: 1259
Abstract HTML Views: 439
PDF Downloads: 432
ePub Downloads: 324
Total Views/Downloads: 2454
Unique Statistics:

Full-Text HTML Views: 676
Abstract HTML Views: 299
PDF Downloads: 323
ePub Downloads: 245
Total Views/Downloads: 1543



Creative Commons License
© 2023 Praditpod et al.

open-access license: This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International Public License (CC-BY 4.0), a copy of which is available at: https://creativecommons.org/licenses/by/4.0/legalcode. This license permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

* Address correspondence to this author at the Department of Biomedical Engineering, School of Science and Engineering, University of Dundee, Dundee, United Kingdom; Tel.: (+44)1382386730; E-mail c.li@dundee.ac.uk


Abstract

Background:

Motion variance differs among individuals, knowing as the differences in dominant and non-dominant hand functions provide beneficial information to clinicians or therapists regarding accurate diagnosis and rehabilitation purposes. However, due to subjective considerations, there are some limitations of the handedness questionnaires, which are one of the standard methods for evaluating interlimb function differences.

Objective:

This study aims to quantify the differences in upper limb motions between the dominant and non-dominant hands in the reaching task using approximate entropy (ApEn) and sample entropy (SampEn) measures. This study also provides proper combinations of parameter values m and r for the ApEn and SampEn measures in the hand movement data of the reaching task.

Methods:

Twenty volunteers performed a multi-directional reaching task. The acceleration data of hand motions were recorded by GENEActiv 3D acceleration sensor (Activinsights Ltd., UK) with a sampling frequency of 1000 Hz. In addition, the ApEn and SampEn values were analysed.

Results:

The ApEn values of the dominant hand were statistically significantly lower than those of the non-dominant hand for parameter combinations of m=2,3,4,5 with r=0.15,0.20,0.25 for the Y- and Z-axis (p<0.05). The SampEn values of the dominant hand significantly demonstrated lower than those of the non-dominant hand for all axes when computing on combinations of parameter m=2,3,4,5 with r=0.15,0.20 (p<0.05).

Conclusion:

The ApEn and SampEn measures could be used to predict the degree of regularity or complexity of the reaching hand motion time-series data. These entropy measures also reveal the differences between the dominant and non-dominant hand movements, quantifying movement differences in the dynamic motor tasks associated with hemispheric brain asymmetry.

Keywords: Approximate entropy, Sample entropy, Reaching, Acceleration data, Dominant hand, and Non-dominant hand.

1. INTRODUCTION

Reaching, a representative dynamic movement corresponding to handedness has been extensively studied in healthy people and people with diseases [1-10]. It is also one of the significant fundamental tasks of upper limb performances in daily activities. As the brain's two cerebral hemispheres are asymmetrical in structure and function [11, 12]. The demonstration of the hemispheric brain asymmetry to control upper limb movements is commonly known as handedness [13-19].

According to the research of M.P. Bryden [20], there would be no differences between the dominant and non-dominant hands for performing unskilled or simple tasks, e.g., reaching. The preferred hand would perform better than the non-dominant hand for skilled tasks. On the other hand, based on the dynamic dominance model of brain lateralisation, the movement differences of each arm would be observed [17, 21]. The dominant hand movements would be smoother and straighter than those of the non-dominant hand [17]. The relationship between a bias in the preferential use of one hand over another hand and a bias in the skill to perform the task of one hand over the other is still unclear. Researchers have studied the link between hand preference and hand performance related to the lateralisation of motor control mechanisms for each hemispheric asymmetry system. They examined the differences between both hands when performing the reaching tasks to attain an advanced understanding of specialised motor skill lateralisation [17, 20, 22]. In a clinical situation, comparing interlimb functions is crucially recommended to clinicians and therapists and should be cautiously undertaken because the differences in interlimb movements affect physical performance. Comparing dominant and non-dominant hand functions were examined in healthy volunteers and patients regarding accurate diagnosis and rehabilitation purposes [23-30]. The data on handedness ques-tionnaires, which were one of the common methods to evaluate the differences between the dominant and non-dominant hand functions, is required to give more accuracy in rating the functionality scales because of its natural subjective considerations [25, 27]. Therefore, investigating the quanti-tative data of the differences between the dominant and non-dominant hand motions is essential.

The imaging technologies, e.g., functional MRI [31, 32], one of the most widely used methods to study a function of hemispheric brain asymmetry, have some limitations in evaluating a dynamic movement, e.g., motion artifact [15, 19]. In measuring the characteristics of reaching and exploring arm-hemispheric asymmetry, many studies have examined the quantification of reaching using various variables of kinematics [17, 19] and kinetics techniques [13]. Nevertheless, there is still a lack of studies investigating the complexity and chaotic behaviour of the acceleration time-series data when performing the reaching task between the dominant and non-dominant hand movements by using entropy measures. Approximate entropy (ApEn) and sample entropy (SampEn) are two popular entropy measurement methods in time domain analysis to investigate the predictability and complexity of the time-series data. These two entropy measures have now been broadly applied in many studies regarding quantifying complexity measures in several biological time-series signals [33], e.g., the centre of pressure [34-39] and heart rate [40, 41].

The computation of ApEn and SampEn values is dependent on the input parameters m (length of subseries data), r (tolerance of similarity), and N (length of signal data) [38, 39]. The input parameter m=1,2,3 and the use of r values between 0.10-0.25 multiply the standard deviation (SD) of the time-series data was traditionally recommended to calculate the ApEn and SampEn values because of producing good statistical validity of entropy for predicting the randomness of the clinical data, e.g., respiratory and cardiovascular data [34, 42-45]. Nevertheless, these recommendations do not always bring about optimal entropy values for other data types. Moreover, there are no clear instructions and standard guidelines on what input parameter values should be selected for other types of time-series data to measure the regularity and complexity of the signals using the ApEn and SampEn [38, 39]. So, each study of biological signals should also examine their own input parameters, m and r, to calculate the ApEn and SampEn values for providing important information.

Currently, there have not been any researches that study the parameter combinations m and r to examine the differences in the entropy analysis of reaching through the motion time-series data. This study aims to examine the differences in the three-axis acceleration time-series data of the upper limb motions between the dominant and non-dominant hands in the reaching task using the ApEn and SampEn measures. This study will provide information for future research regarding the studies of handedness or arm laterality in controlling movements in the reaching task and also provide the combinations of parameter values m and r for the ApEn and SampEn measures in the hand movement data of the reaching task.

2. MATERIALS AND METHODS

2.1. Participants

Twenty volunteers (10 males and females) aged between 24-40 years participated in the study. They had no history of neurological diseases and musculoskeletal impairments of the upper limbs, which could interfere with task performance. The handedness of participants was assessed by the Edinburgh inventory [46]. Nineteen volunteers were right-handed, and one was left-handed. Before starting the experiment, the participant information sheet was provided to all participants, and they then signed a consent form. The ethical approval was proved by the School Research Ethics Committee of the School of Science and Engineering, University of Dundee (UOD-SSEREC-BE-RPG-2019-006).

2.2. Reaching Task Design

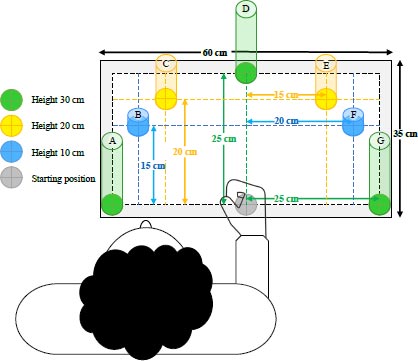
As reaching is essential in daily activities, this study then designed a simulated task for reaching in three-dimensional space to measure the movement differences between both arms [47-49]. The mimic three-dimensional reaching task was modified from moving hands on a dimensional board in Praditpod’s study [50]. Seven pillars with different heights were placed on the board with different locations to provide multi-directional reaching movements to represent hand movements in everyday manual activities. The details of the height and location of each pillar on the board are shown in Fig. (1).

2.3. Procedure

The participants wore a wearable sensor on both wrists throughout the experimental period. Before starting the experiment, they placed their hand on a starting point (a grey marker) on the board with a side fist position (Fig. 1). The researcher demonstrated the sequences of the reaching task to them for one trial. They were then introduced to perform the reaching task on both hands and were trained on the task by watching a video and/or handout, which illustrated the sequences of the reaching task.

Fig. (1). Seven pillars with different heights were placed in different locations on the board. Subjects sat upright on a chair with their elbow in flexion 90o position and their upper arm and the middle pillar (pillar D) in a line.

They were asked to perform the reaching task as fast and smoothly as possible. Reaching movements were also recorded by video recorder during the experiment. The participants’ faces were not captured to preserve their privacies. The sequences of the reaching task are described in Appendix A.

2.4. Data Analysis

A commercial three-dimensional accelerometer sensor, the GENEActiv accelerometer sensor (Activinsights Ltd., UK), recorded the motion data of the reaching task. The acceleration data were recorded at a frequency of 1000 Hz to avoid losing the important data of the motion signals [51] and to generate the time-series data to be closer to the actual movements as well as to prevent aliasing when doing signal processing as the frequency of reaching is still unknown. The data were extracted and downloaded from the sensor via GENEActiv PC software once the recording of hand motions was complete. The derivative acceleration data were imported to MATLAB software (Version 9.2, MathWorks, USA) for entropy analysis.

2.4.1. Entropy Measures

Entropy is an idea that addresses information related to the predictability and randomness of the dynamic system. This study employed the approximate entropy (ApEn) and sample entropy (SampEn) as the methods for entropy estimation of the hand motion time-series data.

Pincus introduced a set of data complexity measurements, which is called approximate entropy, that is easily applied to short and noisy time-series data of clinical biological signals [43, 52, 53]. The concept of the ApEn is that the N length of time-series data is divided into the m length of embedding vectors, which are called a template vector and a compared vector. After that, the similarity of these two vectors is compared. The template vector is compared with all the next following vectors in the sequences. Those two compared vectors containing m data points and having a range from 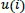to 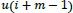are generated as:

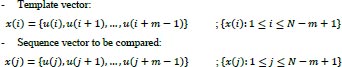Then, the maximum difference of distance between the template vector, 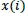, and the compared vector, 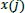, is calculated by computing component-by-component of all their corresponding scalar components as follows:

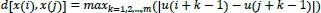If the distance difference between each scalar component of 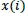and 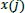is less than or equal to the value of r, those compared vectors are considered as “possible”. Then, the next component is computed. Consequently, if the distance difference between all scalar components of 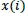and 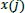meets the required condition that 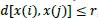those compared vectors are considered as “template match”.

To compute the value of the function 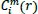, the conditional probabilities are calculated by the total of template matches divided by those of possible vectors as follows:

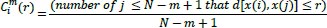(1)

Of the 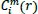calculation, the vector 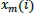is called a template vector, whereas the vector 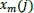within threshold r is called a template match vector. So, 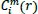is the conditional probability that any vectors 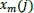are in threshold r of the data set.

The function 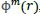, the average of natural logarithms of function 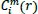, is computed as:

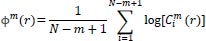(2)

The statistical estimator of the parameter ApEn (m, r) is defined as:

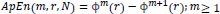(3)

Therefore, the value of ApEn can be approximately calculated as:

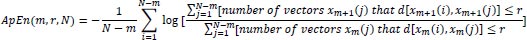(4)

Besides, sample entropy (SampEn), a modified version of the ApEn, is a powerful and useful method to understand, quantify, and measure the complexity or the amount of regularity of a time series of biological signals in experimental clinical studies [43, 44, 53, 54]. 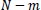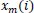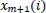Because of the bias of ApEn, to exclude self-matches calculating and consider only the first vectors of length m to ensure that and for 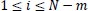were defined. Therefore, Richman and Moorman defined the algorithm of the SampEn as follows [44].

The total number of possible vectors, 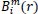, is defined as:

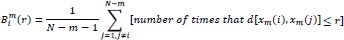(5)

The function 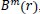which is the conditional probability that two vectors match for m points, is defined as:

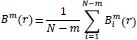(6)

Likewise, the total number of template match vectors, 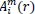, is defined as:

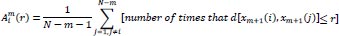(7)

Then, the function 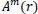, which is the conditional probability that two vectors are similar for m+1 points, is defined as:

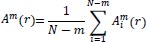(8)

The statistical estimator of the parameter SampEn (m, r) is defined as:

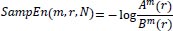(9)

Therefore,

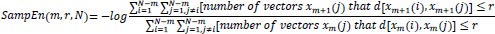(10)

2.5. Statistical Analysis

A Shapiro-Wilk test was used to test for the normality of the ApEn and SampEn values. The statistically significant differences between the dominant and non-dominant hands have been examined through a Paired T-test for normal distribution data and a Wilcoxon Signed Rank test for non-normal distribution data [54-57]. Statistical significance was set at p<0.05.

3. RESULTS

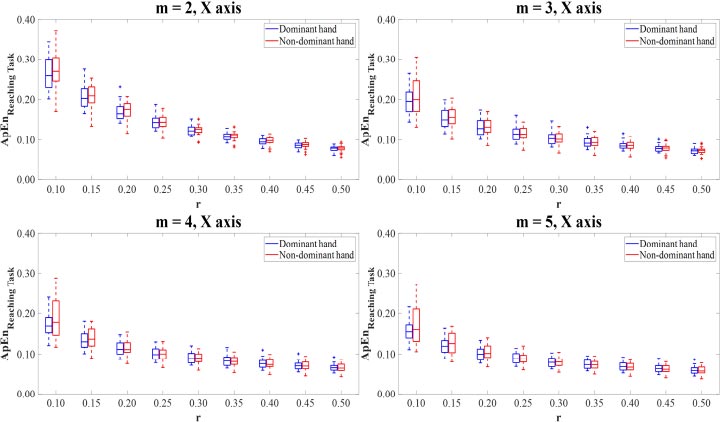
The combinations of parameter values were set m=2,3,4,5 and r=0.10,0.15,0.20,0.25,0.30,0.35,0.40,0.45,0.50 to calculate the ApEn and SampEn values of the motion time-series data. For the multi-directional reaching task, the ApEn and SampEn values were computed on the X-axis, Y-axis, Z-axis, and Vector magnitude of the dominant and non-dominant hand motion time-series data for all thirty-six combinations of parameter values m and r. On the ApEn and SampEn values, low values describe that the time-series signal is less complex and has high predictability, while high values mean that the signal is more complex and has poor predictability.

3.1. Approximate Entropy

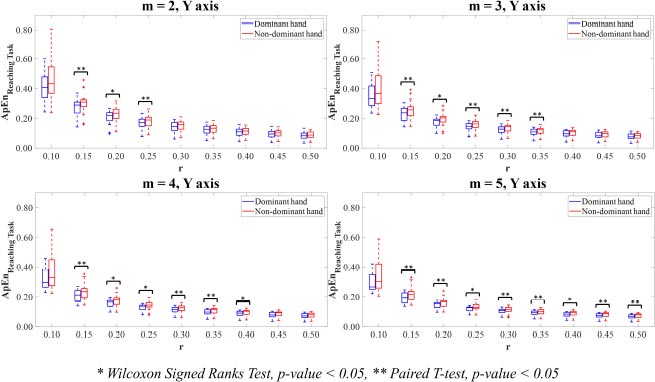
The ApEn values of the dominant and non-dominant movements in terms of mean and standard deviation (SD) are shown in Table 1. The ApEn values of the dominant hand movements were mostly lower than those of non-dominant hand movements. Paired T-test and Wilcoxon Signed Rank test revealed that there were no differences in the ApEn values between the dominant and non-dominant hands on X-axis (Fig. 2). There were significant differences (p<0.05) between the ApEn values for the dominant hand movements compared to the non-dominant hand movements on Y-axis (Fig. 3), Z-axis (Fig. 4), and Vector Magnitude (Fig. 5).

In Y-axis, the dominant hand motion time-series signal showed significantly higher predictability than the non-dominant hand. Statistical analysis showed that those differences were significant for the combinations of parameter values m=2 with r=0.15,0.20,0.25, m=3 with r=0.15,0.20, 0.25,0.30,0.35, m=4 with r=0.15,0.20,0.25,0.30,0.35,0.40, and m=5 with r=0.15,0.20,0.25,0.30,0.35,0.40,0.45,0.50 (p<0.05).

In Z-axis, the motion time-series data of the dominant hand showed lower ApEn values than the non-dominant hand. Of parameter value m=2, the ApEn values computing on the combinations with all parameter values r in the dominant hand were statistically significantly lower than those in the non-dominant hand (p<0.05). The results of parameter values m= 3,4,5 showed that the ApEn values in the dominant hand were statistically significantly lower than those in the non-dominant hand for the combinations with r=0.10,0.15,0.20,0.25,0.30,0.35 (p<0.05).

Table 1. Approximate entropy values in X-axis, Y-axis, Z-axis, and Vector magnitude as a function of the thirty-six input parameter combinations m and r for the dominant and non-dominant hands motion time-series data in terms of mean value and standard deviation.
Approximate entropy values (N = 20)
m r X-axis Y-axis Z-axis Vector magnitude
Dominant hand Non-dominant hand Dominant hand Non-dominant hand Dominant hand Non-dominant hand Dominant hand Non-dominant hand
Mean SD Mean SD Mean SD Mean SD Mean SD Mean SD Mean SD Mean SD
2 0.10 0.2649 0.0419 0.2695 0.0484 0.4185 0.0996 0.4582 0.1329 0.3998* 0.0770 0.4604* 0.1135 0.2556 0.0406 0.2804 0.0652
0.15 0.2066 0.0306 0.2077 0.0307 0.2712** 0.0618 0.3040** 0.0716 0.2658** 0.0379 0.3028** 0.0551 0.1885 0.0270 0.2004 0.0345
0.20 0.1696 0.0228 0.1714 0.0232 0.2070* 0.0473 0.2284* 0.0542 0.2059** 0.0282 0.2244** 0.0380 0.1514 0.0204 0.1590 0.0240
0.25 0.1437 0.0166 0.1447 0.0188 0.1660** 0.0413 0.1817** 0.0426 0.1659** 0.0235 0.1803** 0.0268 0.1276 0.0156 0.1323 0.0183
0.30 0.1233 0.0122 0.1250 0.0149 0.1406 0.0386 0.1516 0.0367 0.1397** 0.0193 0.1514** 0.0228 0.1097 0.0129 0.1136 0.0149
0.35 0.1080 0.0098 0.1098 0.0127 0.1208 0.0342 0.1289 0.0319 0.1215** 0.0175 0.1304** 0.0215 0.0963 0.0107 0.0994 0.0126
0.40 0.0950 0.0084 0.0972 0.0108 0.1053 0.0314 0.1109 0.0275 0.1072** 0.0157 0.1154** 0.0193 0.0854 0.0091 0.0884 0.0113
0.45 0.0850 0.0073 0.0864 0.0097 0.0928 0.0295 0.0980 0.0256 0.0952** 0.0141 0.1022** 0.0175 0.0769 0.0078 0.0794 0.0102
0.50 0.0769 0.0071 0.0777 0.0093 0.0825 0.0268 0.0870 0.0233 0.0858** 0.0134 0.0920** 0.0163 0.0696 0.0069 0.0720 0.0092
3 0.10 0.1947 0.0331 0.2056 0.0481 0.3580 0.0844 0.3934 0.1220 0.3392* 0.0781 0.4029* 0.1103 0.2053** 0.0397 0.2292** 0.0661
0.15 0.1547 0.0250 0.1552 0.0266 0.2283** 0.0452 0.2566** 0.0608 0.2207** 0.0338 0.2582** 0.0500 0.1509 0.0229 0.1606 0.0314
0.20 0.1322 0.0218 0.1319 0.0210 0.1747* 0.0329 0.1948* 0.0444 0.1723** 0.0227 0.1898** 0.0319 0.1222 0.0188 0.1283 0.0205
0.25 0.1165 0.0196 0.1157 0.0183 0.1417** 0.0291 0.1579** 0.0350 0.1407** 0.0175 0.1523** 0.0203 0.1036 0.0160 0.1081 0.0161
0.30 0.1043 0.0169 0.1034 0.0160 0.1217** 0.0289 0.1340** 0.0313 0.1196** 0.0139 0.1286** 0.0170 0.0906 0.0137 0.0945 0.0135
0.35 0.0941 0.0140 0.0937 0.0142 0.1064** 0.0268 0.1165** 0.0280 0.1052** 0.0130 0.1118** 0.0167 0.0808 0.0114 0.0838 0.0117
0.40 0.0856 0.0110 0.0851 0.0122 0.0945 0.0255 0.1022 0.0250 0.0937 0.0132 0.0998 0.0155 0.0730 0.0100 0.0753 0.0103
0.45 0.0781 0.0090 0.0782 0.0105 0.0849 0.0249 0.0914 0.0231 0.0842 0.0127 0.0899 0.0146 0.0666 0.0088 0.0682 0.0093
0.50 0.0717 0.0076 0.0722 0.0094 0.0767 0.0232 0.0815 0.0209 0.0768 0.0123 0.0818 0.0139 0.0610 0.0078 0.0624 0.0088
4 0.10 0.1716 0.0309 0.1856 0.0483 0.3268 0.0757 0.3595 0.1109 0.3112* 0.0766 0.3731* 0.1068 0.1849** 0.0404 0.2095** 0.0649
0.15 0.1334 0.0225 0.1375 0.0266 0.2078** 0.0383 0.2344** 0.0540 0.2010** 0.0336 0.2388** 0.0484 0.1357 0.0232 0.1457 0.0313
0.20 0.1139 0.0186 0.1139 0.0188 0.1586* 0.0268 0.1764* 0.0385 0.1552* 0.0227 0.1736* 0.0301 0.1114 0.0167 0.1154 0.0201
0.25 0.1011 0.0162 0.0995 0.0155 0.1291* 0.0231 0.1431* 0.0292 0.1267* 0.0156 0.1389* 0.0174 0.0945 0.0141 0.0976 0.0150
0.30 0.0913 0.0151 0.0900 0.0139 0.1108** 0.0230 0.1220** 0.0265 0.1090** 0.0121 0.1172** 0.0136 0.0832 0.0134 0.0852 0.0125
0.35 0.0836 0.0144 0.0824 0.0129 0.0968** 0.0215 0.1070** 0.0242 0.0968* 0.0107 0.1019* 0.0131 0.0735 0.0116 0.0760 0.0107
0.40 0.0766 0.0130 0.0758 0.0119 0.0865* 0.0209 0.0946* 0.0222 0.0870 0.0108 0.0910 0.0123 0.0666 0.0104 0.0688 0.0097
0.45 0.0708 0.0111 0.0701 0.0111 0.0782 0.0209 0.0853 0.0209 0.0783 0.0106 0.0817 0.0119 0.0608 0.0092 0.0625 0.0089
0.50 0.0656 0.0095 0.0650 0.0102 0.0713 0.0198 0.0768 0.0194 0.0713 0.0108 0.0747 0.0116 0.0559 0.0082 0.0574 0.0082
5 0.10 0.1556 0.0279 0.1699 0.0466 0.3015 0.0705 0.3302 0.1013 0.2891* 0.0745 0.3467* 0.1008 0.1693** 0.0384 0.1944** 0.0634
0.15 0.1194 0.0205 0.1261 0.0275 0.1934** 0.0336 0.2182** 0.0496 0.1878** 0.0343 0.2245** 0.0479 0.1243** 0.0243 0.1357** 0.0314
0.20 0.1006 0.0171 0.1035 0.0192 0.1472** 0.0231 0.1636** 0.0340 0.1443* 0.0228 0.1629* 0.0296 0.1021 0.0168 0.1071 0.0201
0.25 0.0890 0.0145 0.0889 0.0147 0.1196* 0.0195 0.1323* 0.0251 0.1174** 0.0151 0.1299** 0.0163 0.0879 0.0128 0.0902 0.0152
0.30 0.0806 0.0129 0.0794 0.0122 0.1032** 0.0190 0.1132** 0.0225 0.1010** 0.0120 0.1093** 0.0114 0.0769 0.0110 0.0789 0.0119
0.35 0.0745 0.0122 0.0729 0.0111 0.0906** 0.0177 0.0996** 0.0208 0.0896* 0.0103 0.0949* 0.0109 0.0680 0.0101 0.0704 0.0101
0.40 0.0687 0.0117 0.0674 0.0104 0.0809* 0.0176 0.0885* 0.0194 0.0809 0.0094 0.0850 0.0103 0.0616 0.0094 0.0639 0.0091
0.45 0.0638 0.0113 0.0627 0.0099 0.0729** 0.0177 0.0804** 0.0187 0.0735 0.0090 0.0766 0.0100 0.0563 0.0087 0.0582 0.0083
0.50 0.0596 0.0105 0.0588 0.0096 0.0667** 0.0169 0.0731** 0.0176 0.0676 0.0094 0.0701 0.0100 0.0518 0.0080 0.0535 0.0078
* Wilcoxon Signed Ranks Test, p-value < 0.05,
** Paired T-test, p-value < 0.05
Fig. (2). Approximate entropy values computed on X-axis of motion time-series data of the reaching task for each parameter combinations m and r in dominant (blue boxplot) and non-dominant hand (red boxplot). The boxplots revealed statistical data of ApEn values on minimum, first quartile, median, third quartile, maximum, and outliers values.

Fig. (3). Approximate entropy values computed on Y-axis of motion time-series data of the reaching task for each parameter combinations m and r in dominant (blue boxplot) and non-dominant hand (red boxplot). The boxplots revealed statistical data of ApEn values on minimum, first quartile, median, third quartile, maximum, and outliers values.

Table 2. Sample entropy values in X-axis, Y-axis, Z-axis, and Vector magnitude as a function of the thirty-six input parameter combinations m and r for the dominant and non-dominant hands motion time-series data in terms of mean value and standard deviation.
Sample entropy values (N = 20)
m r X-axis Y-axis Z-axis Vector magnitude
Dominant hand Non-dominant hand Dominant hand Non-dominant hand Dominant hand Non-dominant hand Dominant hand Non-dominant hand
Mean SD Mean SD Mean SD Mean SD Mean SD Mean SD Mean SD Mean SD
2 0.10 0.1396** 0.0318 0.1553** 0.0526 0.3049 0.0837 0.3388 0.1157 0.2915** 0.0786 0.3493** 0.1093 0.1570** 0.0462 0.1819** 0.0729
0.15 0.0967** 0.0193 0.1050** 0.0299 0.1844** 0.0453 0.2122** 0.0581 0.1802** 0.0402 0.2154** 0.0561 0.1027 0.0274 0.1153 0.0397
0.20 0.0747** 0.0143 0.0809** 0.0210 0.1354** 0.0298 0.1546** 0.0411 0.1335** 0.0287 0.1518** 0.0371 0.0762 0.0197 0.0845 0.0270
0.25 0.0611 0.0115 0.0655 0.0158 0.1061** 0.0231 0.1210** 0.0285 0.1041** 0.0205 0.1174** 0.0245 0.0603 0.0154 0.0663 0.0205
0.30 0.0516** 0.0094 0.0549** 0.0124 0.0887** 0.0201 0.1001** 0.0232 0.0856** 0.0154 0.0960** 0.0177 0.0495 0.0127 0.0544 0.0164
0.35 0.0446** 0.0079 0.0477** 0.0106 0.0756** 0.0165 0.0851** 0.0188 0.0733** 0.0130 0.0810** 0.0142 0.0417 0.0109 0.0456 0.0136
0.40 0.0389** 0.0067 0.0418** 0.0090 0.0659** 0.0143 0.0734** 0.0160 0.0638** 0.0112 0.0706** 0.0120 0.0358 0.0095 0.0391 0.0115
0.45 0.0345** 0.0060 0.0371** 0.0077 0.0582** 0.0131 0.0650** 0.0145 0.0560** 0.0094 0.0618** 0.0098 0.0311 0.0084 0.0340 0.0100
0.50 0.0310** 0.0053 0.0332** 0.0067 0.0520** 0.0114 0.0576** 0.0120 0.0500** 0.0084 0.0552** 0.0083 0.0274 0.0075 0.0300 0.0088
3 0.10 0.1166** 0.0306 0.1345** 0.0519 0.2689 0.0719 0.2995 0.1070 0.2567** 0.0753 0.3163** 0.1057 0.1339** 0.0441 0.1589** 0.0691
0.15 0.0793** 0.0178 0.0884** 0.0287 0.1556** 0.0347 0.1796** 0.0500 0.1521** 0.0365 0.1870** 0.0511 0.0868 0.0250 0.0979 0.0357
0.20 0.0620** 0.0125 0.0676** 0.0196 0.1122** 0.0215 0.1284** 0.0337 0.1109** 0.0252 0.1282** 0.0322 0.0649 0.0173 0.0715 0.0232
0.25 0.0518 0.0101 0.0553 0.0146 0.0874** 0.0163 0.1002** 0.0225 0.0862** 0.0172 0.0979** 0.0200 0.0518 0.0136 0.0565 0.0172
0.30 0.0446 0.0085 0.0472 0.0115 0.0731** 0.0143 0.0831** 0.0181 0.0711** 0.0128 0.0796** 0.0139 0.0430 0.0114 0.0467 0.0137
0.35 0.0393 0.0075 0.0416 0.0098 0.0626** 0.0120 0.0713** 0.0148 0.0611** 0.0105 0.0671** 0.0110 0.0367 0.0098 0.0396 0.0113
0.40 0.0349 0.0066 0.0369 0.0083 0.0550** 0.0107 0.0620** 0.0128 0.0534** 0.0089 0.0586** 0.0092 0.0318 0.0086 0.0343 0.0096
0.45 0.0314 0.0059 0.0331 0.0072 0.0489** 0.0100 0.0552** 0.0117 0.0470** 0.0075 0.0515** 0.0075 0.0279 0.0076 0.0301 0.0083
0.50 0.0285 0.0052 0.0301 0.0063 0.0441** 0.0088 0.0493** 0.0099 0.0422** 0.0069 0.0462** 0.0064 0.0248 0.0068 0.0267 0.0073
4 0.10 0.1091** 0.0304 0.1282** 0.0514 0.2560 0.0673 0.2847 0.1027 0.2428** 0.0736 0.3035** 0.1041 0.1246** 0.0434 0.1495** 0.0676
0.15 0.0726** 0.0181 0.0825** 0.0290 0.1443* 0.0301 0.1669* 0.0456 0.1408** 0.0352 0.1759** 0.0492 0.0796 0.0253 0.0949 0.0461
0.20 0.0559** 0.0124 0.0621** 0.0198 0.1021** 0.0173 0.1169** 0.0294 0.1010** 0.0243 0.1182** 0.0306 0.0594 0.0172 0.0655 0.0220
0.25 0.0465 0.0097 0.0502 0.0145 0.0790** 0.0128 0.0901** 0.0191 0.0777** 0.0163 0.0892** 0.0184 0.0476 0.0131 0.0516 0.0161
0.30 0.0402 0.0079 0.0427 0.0112 0.0660** 0.0113 0.0745** 0.0150 0.0639** 0.0122 0.0720** 0.0123 0.0396 0.0108 0.0427 0.0127
0.35 0.0357 0.0069 0.0377 0.0095 0.0564** 0.0094 0.0640** 0.0123 0.0550** 0.0100 0.0605** 0.0097 0.0339 0.0093 0.0363 0.0105
0.40 0.0319 0.0062 0.0337 0.0081 0.0495** 0.0085 0.0558** 0.0106 0.0482** 0.0085 0.0528** 0.0082 0.0295 0.0083 0.0315 0.0089
0.45 0.0290 0.0057 0.0305 0.0070 0.0440** 0.0079 0.0499** 0.0098 0.0427** 0.0070 0.0463** 0.0067 0.0260 0.0074 0.0278 0.0077
0.50 0.0265 0.0052 0.0278 0.0062 0.0397** 0.0072 0.0448** 0.0084 0.0383** 0.0063 0.0416** 0.0057 0.0232 0.0066 0.0248 0.0068
5 0.10 0.1046** 0.0295 0.1235** 0.0496 0.2460 0.0657 0.2736 0.1012 0.2339** 0.0724 0.2937** 0.1030 0.1186** 0.0419 0.1425** 0.0659
0.15 0.0687** 0.0180 0.0793** 0.0291 0.1380* 0.0276 0.1593* 0.0429 0.1346** 0.0351 0.1691** 0.0482 0.0752** 0.0252 0.0863** 0.0339
0.20 0.0522** 0.0125 0.0590** 0.0202 0.0964** 0.0150 0.1102** 0.0269 0.0956** 0.0244 0.1124** 0.0297 0.0557 0.0174 0.0619 0.0217
0.25 0.0430** 0.0097 0.0473** 0.0148 0.0738** 0.0106 0.0841** 0.0170 0.0727** 0.0162 0.0841** 0.0178 0.0446 0.0130 0.0485 0.0158
0.30 0.0370 0.0077 0.0398 0.0114 0.0615** 0.0093 0.0691** 0.0132 0.0595** 0.0122 0.0675** 0.0118 0.0373 0.0105 0.0400 0.0124
0.35 0.0328 0.0065 0.0349 0.0095 0.0525** 0.0078 0.0591** 0.0108 0.0510** 0.0098 0.0565** 0.0090 0.0319 0.0089 0.0340 0.0101
0.40 0.0295 0.0057 0.0312 0.0080 0.0460** 0.0072 0.0515** 0.0092 0.0447** 0.0084 0.0492** 0.0076 0.0278 0.0079 0.0296 0.0086
0.45 0.0269 0.0053 0.0282 0.0069 0.0409** 0.0067 0.0461** 0.0085 0.0395** 0.0070 0.0431** 0.0062 0.0246 0.0071 0.0261 0.0074
0.50 0.0247 0.0049 0.0258 0.0061 0.0369** 0.0060 0.0415** 0.0074 0.0356** 0.0062 0.0387** 0.0053 0.0220 0.0064 0.0233 0.0066
* Wilcoxon Signed Ranks Test, p-value < 0.05,
** Paired T-test, p-value < 0.05
Fig. (4). Approximate entropy values computed on Z-axis of motion time-series data of the reaching task for each parameter combinations m and r in dominant (blue boxplot) and non-dominant hand (red boxplot). The boxplots revealed statistical data of ApEn values on minimum, first quartile, median, third quartile, maximum, and outliers values.

Fig. (5). Approximate entropy values computed on Vector Magnitude of motion time-series data of the reaching task for each parameter combinations m and r in dominant (blue boxplot) and non-dominant hand (red boxplot). The boxplots revealed statistical data of ApEn values on minimum, first quartile, median, third quartile, maximum, and outliers values.

Fig. (6). Sample entropy values computed on X-axis of motion time-series data of the reaching task for each parameter combinations m and r in dominant (blue boxplot) and non-dominant hand (red boxplot). The boxplots revealed statistical data of SampEn values on minimum, first quartile, median, third quartile, maximum, and outliers values.

Fig. (7). Sample entropy values computed on Y-axis of motion time-series data of the reaching task for each parameter combinations m and r in dominant (blue boxplot) and non-dominant hand (red boxplot). The boxplots revealed statistical data of SampEn values on minimum, first quartile, median, third quartile, maximum, and outliers values.

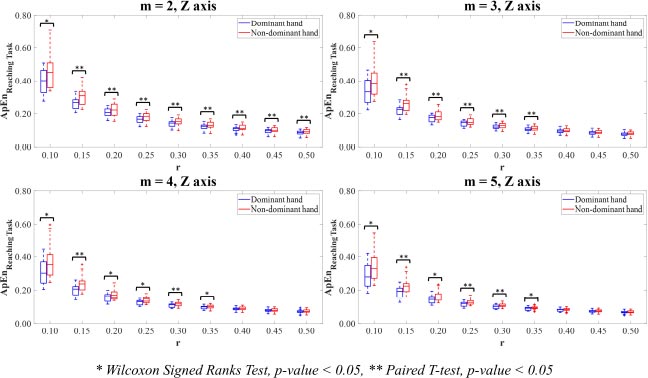
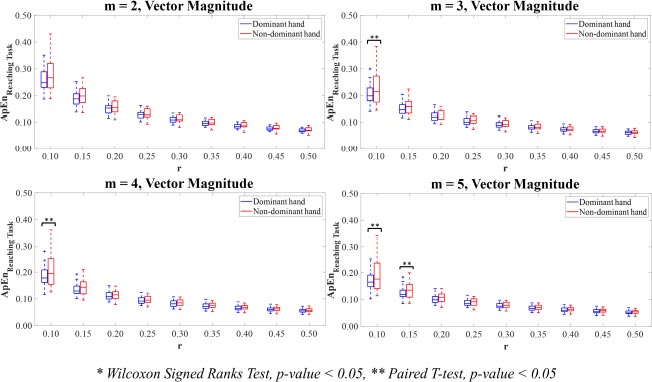
For Vector Magnitude, the motion time-series data of the dominant hand showed lower ApEn values than the non-dominant hand. The statistically significant differences in the ApEn values between the dominant and non-dominant hands were only observed in the combinations of parameter values m=3,4 with r=0.10 and m=5 with r=0.10,0.15 (p<0.05).

3.2. Sample Entropy

The SampEn values of the dominant and non-dominant movements in terms of mean and standard deviation (SD) are shown in Table 2. The SampEn values of the dominant hand movements were entirely lower than those of the non-dominant hand movements. The Paired T-test and Wilcoxon Signed Rank test indicated significant differences (p<0.05) between the SampEn values of the dominant and non-dominant hand movements in all axes.

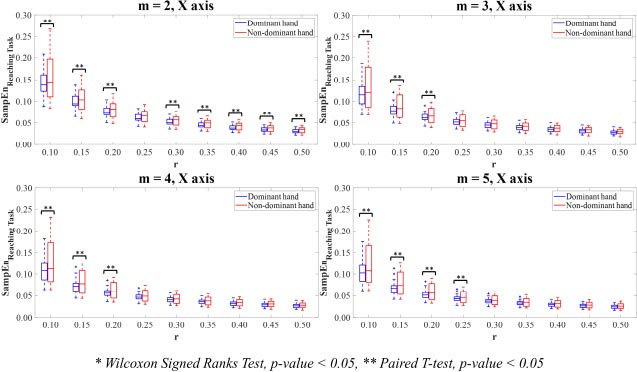
In X-axis (Fig. 6), the SampEn values computing on the combinations of parameter value m=2 with all parameter values r, except r=0.25, in the dominant hand was statistically significantly lower than those in the non-dominant hand (p<0.05). A statistically significant difference was found between the SampEn values of the dominant and non-dominant hands for the combinations of parameter values m=3 with r=0.10,0.15,0.20 (p<0.05). For parameter values m=4,5, the SampEn values of the dominant hand significantly demonstrated lower than the non-dominant hand when combined with parameter values r=0.10,0.15,0.20 and r=0.10,0.15,0.20,0.25 for m=4,5, respectively (p<0.05).

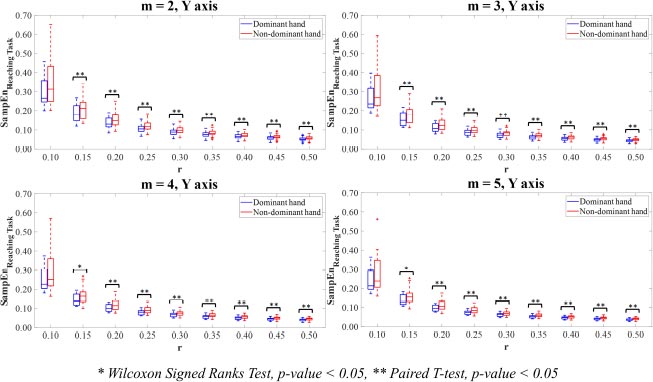
In Y-axis (Fig. 7), all parameter value combinations m and r, excluding the combinations of parameter values m=2,3,4,5 with r=0.10, had significant differences between the hand motion time-series data of the dominant and non-dominant hands (p<0.05).

Moreover, the significant differences in the SampEn values between the dominant and non-dominant hands were found on Z-axis for all parameter value combinations m and r (p<0.05) (Fig. 8).

For Vector Magnitude (Fig. 9), there were only significant differences between the SampEn values for the dominant hand compared to the non-dominant hand for the combinations of parameter values m=2,3,4 with r=0.10 and m=5 with r=0.10,0.15 (p<0.05).

4. DISCUSSION AND FURTHER STUDY

The current study aims to assess the differences in the degree of complexity and regularity of hand movements between the dominant and non-dominant hands when performing the reaching task. For this goal, the hand motion time-series data of the reaching task of healthy subjects have been analysed by the ApEn and SampEn, which are widely used to evaluate the degree of complexity of physiological signals in terms of considering the dynamics of point-to-point time-series data [34, 38-40, 43-45, 52, 58-62].

In previous studies, the reaching movements, which have been applied to a wide range of research to explore the difference between dominant and non-dominant movements, were performed in the horizontal plane [13, 19, 63-67]. Although some studies showed that subjects could freely move in all directions, the reaching movements still have a limitation in the vertical plane due to the experiment setup [66]. Compared with previous studies, the current reaching task has advantages over the previous reaching tasks. The current task is designed to encourage subjects to perform hand motions in both horizontal and vertical planes and allow them to move in all directions of three-dimension space without limited movements.

The significant differences in the entropy measures in this study markedly provide useful information regarding lower entropy values, especially the SampEn values, of the dominant hand compared to the non-dominant hand for the reaching task. In other words, it could be indicated that the dominant hand movements are more regular than the non-dominant hand. The dominant hand generally reflects more efficient motor control (greater manual dexterity) than the non-dominant hand [13, 68-72]. The more regularity observed in the dominant hand movements might associate with the effects of the central nervous system (CNS) that controls the ability of intersegmental dynamics and body movements regarding a mechanism of distinct neural control [69, 72]. Moreover, the reason to support the findings of this study could be that most participants in this study are right-handed, and the left-brain hemisphere of a right-handed person plays a greater role in controlling the movements [16, 32]. According to the natural assumption of hemispheric brain asymmetry in motor lateralisation, several studies supported that the dominant hand was generally better than the non-dominant hand in proficiency in performing the tasks [19, 22]. The findings of differences between entropy values of the dominant and non-dominant hands in this study correspond with the results of previous studies that examined the differences between the dominant and non-dominant hands in various features, e.g., muscle torque and electromyography [69], movement path [13, 72], handgrip strength [73, 74].

This study also examines the ability of ApEn and SampEn measures to evaluate the complexity of the motion time-series data. The results show that the ApEn and SampEn are reliable methods for analysing the complexity of the hand motion time-series data and describing the significant difference in the time-series data between the dominant and non-dominant hand movements. From a statistical testing perspective, the dominant hand movements on the X-axis, Y-axis, Z-axis, and Vector Magnitude of the reaching task show generally lower ApEn values than the non-dominant hand movements. Of the SampEn measure, the results highlight that the movements of the dominant hand showed entirely lower complexity than those of the non-dominant hand for all parameter combinations for all axes and Vector Magnitude. Previous studies supported these findings, which found that the SampEn demonstrated high ability and consistency for the complexity measures without crossover issues as an advantage of the SampEn over the ApEn [38, 44, 45, 75, 76]. Compared with other studies, similar behaviour of the ApEn and SampEn values has been observed in this study for all parameter value combinations. For a selected parameter value m, the ApEn and SampEn values tend to decrease as r values increase. Similarly, for a selected parameter value r, the ApEn and SampEn values tend to decrease as m values increase [38, 39].

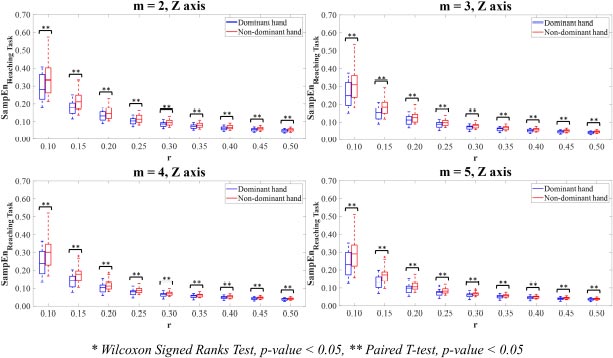
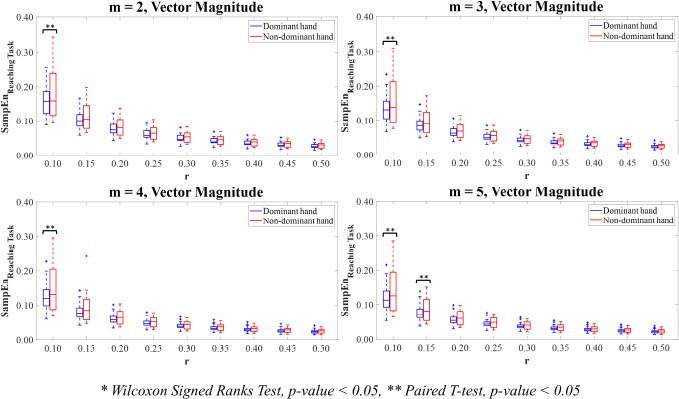
Fig. (8). Sample entropy values computed on Z-axis of motion time-series data of the reaching task for each parameter combinations m and r in dominant (blue boxplot) and non-dominant hand (red boxplot). The boxplots revealed statistical data of SampEn values on minimum, first quartile, median, third quartile, maximum, and outliers values.

Fig. (9). Sample entropy values computed on Vector Magnitude of motion time-series data of the reaching task for each parameter combinations m and r in dominant (blue boxplot) and non-dominant hand (red boxplot). The boxplots revealed statistical data of SampEn values on minimum, first quartile, median, third quartile, maximum, and outliers values.

Additionally, these initial results have proved the importance of chosen parameter value combinations m and r in recognising the significant differences between experimental groups. Based on entropy computations with parameter values m=2,3,4,5 with r values between 0.10-0.50 times SD of the hand motion data, the findings allow the researchers to narrow down the choices of potential values of parameter combinations m and r in case of using the ApEn and SampEn for calculating the complexity of the hand movements. Also, the suggestions from the previous study proposed that the low value of parameter m is recommended, and the parameter value r requires a large number enough to ensure that the amount of sequences of vectors within tolerance r is adequate to estimate the conditional probabilities [45]. From the statistical perspective, the chosen combinations of parameter values m=2,3,4,5 with r=0.15,0.20,0.25 reveal the significant differences between the ApEn values on Y-axis and Z-axis (p<0.05). To reveal the significant differences between the SampEn values on all axes (p<0.05), the chosen parameter value combinations m=2,3,4,5 with r=0.15,0.20 are employed. Noticeably, it could be observed that the SamEn potentially produces more significant differences between the dominant and non-dominant hands than the ApEn for the most axis of reaching movements.

For further studies, researchers who are interested in estimating the complexity levels of motion time-series signals may favour the SampEn measure over the ApEn measure when dealing with the complexity analysis of the physiological time-series data [38, 44, 45, 75, 76]. For the ApEn measure, parameter value combinations m=2,3,4,5 with r=0.15,0.20,0.25 are suggested for analysing the reaching data. Of the SampEn measure, the chosen parameter value combinations m=2,3,4,5 with r=0.15,0.20 are suggested for analysing the reaching data to reveal the movement differences in all axes. Moreover, this study also provides the multi-directional reaching task, which could be a useful and functional diagnosis as well as an assessment tool for further research that would like to study motions in healthy and patient groups.

CONCLUSION

In summary, the current findings suggest that the entropy values of the dominant hand movements are lower than those of the non-dominant hand movements representing less complex and highly predictable dominant hand movements. Furthermore, the ApEn and SampEn measures can estimate the degree of regularity or complexity of the hand motion time-series data for the reaching task and reveal the differences between the dominant and non-dominant hand movements. Interestingly, the relative consistency results and the ability to distinguish the differences between interlimb movements were mostly observed in the SampEn measure, enhancing the advantage of the SampEn over the ApEn when dealing with the hand motion time-series data.

LIST OF ABBREVIATIONS
ApEn = Approximate Entropy
SampEn = Sample Entropy
SD = Standard Deviation

AUTHORS’ CONTRIBUTIONS

- Supervision: Chunhui Li, Zhihong Huang

- Conception and design of the study: Nuttaporn Praditpod, Chunhui Li, Zhihong Huang, Phongpan Tantipoon,

- Methodology: Nuttaporn Praditpod, Chunhui Li, Zhihong Huang, Phongpan Tantipoon

- Data acquisition: Nuttaporn Praditpod, Phongpan Tantipoon

- The conception of statistical analysis: Xinyu Zhang, Petra Rauchhaus

- Data analysis: Nuttaporn Praditpod, Phongpan Tantipoon

- Data interpretation: Nuttaporn Praditpod, Chunhui Li, Phongpan Tantipoon

- The original draft of the manuscript: Nuttaporn Praditpod, Phongpan Tantipoon

- Revising and editing the manuscript: Nuttaporn Praditpod, Chunhui Li, Phongpan Tantipoon

All authors have read and concurred with the content in the final version of the manuscript to be submitted.

ETHICS APPROVAL AND CONSENT TO PARTICIPATE

The ethical approval was proved by the School Research Ethics Committee of the School of Science and Engineering, University of Dundee (UOD-SSFRFC-BE-RPG-2019-006).

HUMAN AND ANIMAL RIGHTS

No animals were used in this research. All procedures performed in studies involving human participants were in accordance with the ethical standards of institutional and/or research committees and with the 1975 Declaration of Helsinki, as revised in 2013.

CONSENT FOR PUBLICATION

Before starting the experiment, the participant information sheet was provided to all participants, and they then signed a consent form. Participants can decide to stop participating in this study at any time without explanation or penalty and do not have to give a reason.

STANDARDS OF REPORTING

STROBE guidelines were followed.

AVAILABILITY OF DATA AND MATERIALS

The data that support the findings of this study are available from the corresponding author, [C.L], only on special request.

FUNDING

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors. NP and PT work at Thammasat University, Thailand. XZ, PR, CL, and ZH work at the University of Dundee, UK.

CONFLICT OF INTEREST

The authors declare no conflict of interest.

Appendix A

The sequences of mimic reaching task in order to touch all seven targets in different directions were as follows:

Starting Place hand with side fist position on a starting point

Step 1 Move hand to the pillar A and fully place hand on the top of pillar, then back to the starting point

Step 2 Move hand to the pillar C and fully place hand on the top of pillar, then back to the starting point

Step 3 Move hand to the pillar F and fully place hand on the top of pillar, then back to the starting point

Step 4 Move hand to the pillar D and fully place hand on the top of pillar, then back to the starting point

Step 5 Move hand to the pillar G and fully place hand on the top of pillar, then back to the starting point

Step 6 Move hand to the pillar E and fully place hand on the top of pillar, then back to the starting point

Step 7 Move hand to the pillar B and fully place hand on the top of pillar, then back to the starting point as the end position

ACKNOWLEDGEMENTS

The authors would like to thank all volunteers for participating in the study. NP and PT are supported by a studentship provided by Royal Thai Government Scholarship and Thammasat University, Thailand. NP is also partially supported by the Funds for Women Graduates Foundation, UK.

REFERENCES

[1] M.C. Cirstea, and M.F. Levin, "Compensatory strategies for reaching in stroke", Brain, vol. 123, no. 5, pp. 940-953, 2000.
[2] P.H. McCrea, J.J. Eng, and A.J. Hodgson, "Biomechanics of reaching: clinical implications for individuals with acquired brain injury", Disabil. Rehabil., vol. 24, no. 10, pp. 534-541, 2002.
[3] J.M. Wagner, C.E. Lang, S.A. Sahrmann, D.F. Edwards, and A.W. Dromerick, "Sensorimotor impairments and reaching performance in subjects with poststroke hemiparesis during the first few months of recovery", Phys. Ther., vol. 87, no. 6, pp. 751-765, 2007.
[4] Y. Tomita, N.A. Turpin, D. Piscitelli, A.G. Feldman, and M.F. Levin, "Stability of reaching during standing in stroke", J. Neurophysiol., vol. 123, no. 5, pp. 1756-1765, 2020.
[5] L.E. Kahn, M.L. Zygman, W.Z. Rymer, and D.J. Reinkensmeyer, "Robot-assisted reaching exercise promotes arm movement recovery in chronic hemiparetic stroke: a randomized controlled pilot study", J. Neuroeng. Rehabil., vol. 3, no. 1, p. 12, 2006.
[6] R.C.V. Loureiro, and W.S. Harwin, "Reach & Grasp Therapy: Design and Control of a 9-DOF Robotic Neuro-rehabilitation System", 2007 IEEE 10th International Conference on Rehabilitation Robotics, pp. 757-763, 2007.
[7] M.D. Ellis, T.M. Sukal-Moulton, and J.P.A. Dewald, "Impairment-based 3-D robotic intervention improves upper extremity work area in chronic stroke: targeting abnormal joint torque coupling with progressive shoulder abduction loading", IEEE Transac Robot, vol. 25, no. 3, pp. 549-555, 2009.
[8] A.E. Jackson, P.R. Culmer, M.C. Levesley, J.A. Cozens, S.G. Makower, and B.B. Bhakta, "Effector force requirements to enable robotic systems to provide assisted exercise in people with upper limb impairment after stroke", IEEE Int. Conf. Rehabil. Robot., vol. 2011, pp. 1-6, 2011.
[9] A.M. Acosta, H.A. Dewald, and J.P.A. Dewald, "Pilot study to test effectiveness of video game on reaching performance in stroke", J. Rehabil. Res. Dev., vol. 48, no. 4, pp. 431-444, 2011.
[10] A. Pacilli, M. Germanotta, S. Rossi, and P. Cappa, "Quantification of age-related differences in reaching and circle-drawing using a robotic rehabilitation device", Appl. Bionics Biomech., vol. 11, no. 3, pp. 91-104, 2014.
[11] B. Hanna-Pladdy, J.E. Mendoza, G.T. Apostolos, and K.M. Heilman, "Lateralised motor control: hemispheric damage and the loss of deftness", J. Neurol. Neurosurg. Psychiatry, vol. 73, no. 5, pp. 574-577, 2002.
[12] Y. Sun, J. Li, J. Suckling, and L. Feng, "Asymmetry of hemispheric network topology reveals dissociable processes between functional and structural brain connectome in community-living elders", Front. Aging Neurosci., vol. 9, p. 361, 2017.
[13] R.L. Sainburg, and D. Kalakanis, "Differences in control of limb dynamics during dominant and nondominant arm reaching", J. Neurophysiol., vol. 83, no. 5, pp. 2661-2675, 2000.
[14] R. Sainburg, "Evidence for a dynamic-dominance hypothesis of handedness", Exp. Brain Res., vol. 142, no. 2, pp. 241-258, 2002.
[15] G.A. Ghacibeh, R. Mirpuri, V. Drago, Y. Jeong, K.M. Heilman, and W.J. Triggs, "Ipsilateral motor activation during unimanual and bimanual motor tasks", Clin. Neurophysiol., vol. 118, no. 2, pp. 325-332, 2007.
[16] D.J. Goble, and S.H. Brown, "The biological and behavioral basis of upper limb asymmetries in sensorimotor performance", Neurosci. Biobehav. Rev., vol. 32, no. 3, pp. 598-610, 2008.
[17] E.L. Nelson, N.E. Berthier, and G.D. Konidaris, "Handedness and Reach-to-Place Kinematics in Adults: Left-Handers Are Not Reversed Right-Handers", J. Mot. Behav., vol. 50, no. 4, pp. 381-391, 2018.
[18] E.J. Woytowicz, K.P. Westlake, J. Whitall, and R.L. Sainburg, "Handedness results from complementary hemispheric dominance, not global hemispheric dominance: evidence from mechanically coupled bilateral movements", J. Neurophysiol., vol. 120, no. 2, pp. 729-740, 2018.
[19] X. Xiao, H. Hu, L. Li, and L. Li, "Comparison of dominant hand to non-dominant hand in conduction of reaching task from 3D kinematic data: Trade-off between successful rate and movement efficiency", Math. Biosci. Eng., vol. 16, no. 3, pp. 1611-1624, 2019.
[20] P.J. Bryden, "The influence of M. P. Bryden’s work on lateralization of motor skill: Is the preferred hand selected for and better at tasks requiring a high degree of skill?", Laterality, vol. 21, no. 4-6, pp. 312-328, 2016.
[21] R.L. Sainburg, "Convergent models of handedness and brain lateralization", Front. Psychol., vol. 5, 2014.
[22] P.K. Mutha, K.Y. Haaland, and R.L. Sainburg, "Rethinking motor lateralization: specialized but complementary mechanisms for motor control of each arm", PLoS One, vol. 8, no. 3, p. e58582, 2013.
[23] C. A. Armstrong, and J. A. Oldham, "A comparison of dominant and non-dominant hand strengths", J. Hand Surg., vol. 24, no. 4, 1999.
[24] D.G. Kline, "The Hand. Fundamentals of Therapy, 3rd Editionby J. Boscheinen-Morrin and W. B. Connolly, 243 pp., ill., Oxford, Butterworth-Heinemann, 2001, $49.50", Muscle Nerve, vol. 25, no. 3, pp. 469-469, 2002.
[25] I.C.B. Mcsp, and J.A. Dipcot, "A comparison of dominant and non-dominant hand function in both right- and left-handed individuals using the southampton hand assessment procedure (SHAP)", Br. J. Hand Ther., vol. 8, no. 1, pp. 4-10, 2003.
[26] A. Özcan, Z. Tulum, L. Pınar, and F. Başkurt, "Comparison of pressure pain threshold, grip strength,dexterity and touch pressure of dominant and non-dominant hands within and between right-and left-handed subjects", J. Korean Med. Sci., vol. 19, no. 6, pp. 874-878, 2004.
[27] S.M. Scharoun, and P.J. Bryden, "Hand preference, performance abilities, and hand selection in children", Front. Psychol., vol. 5, p. 82, 2014.
[28] C. Bishop, P. Read, J. Lake, S. Chavda, and A. Turner, "Interlimb asymmetries: Understanding how to calculate differences from bilateral and unilateral tests", Strength Condit. J., vol. 40, no. 4, pp. 1-6, 2018.
[29] R. Nataraj, S. Sanford, M. Liu, and N. Y. Harel, "Hand dominance in the performance and perceptions of virtual reach control", Acta Psychol, vol. 223, p. 103494, 2022.
[30] S.A. Abdel Hamid, M.M.I. Ismaeel, and E.E. Salem, "Differences in Manual Dexterity between Dominant and Non-Dominant Side in Typically Developed Children", Egypt. J. Hosp. Med., vol. 87, no. 1, pp. 1317-1321, 2022.
[31] S.M. Rao, J.R. Binder, P.A. Bandettini, T.A. Hammeke, F.Z. Yetkin, A. Jesmanowicz, L.M. Lisk, G.L. Morris, W.M. Mueller, L.D. Estkowski, E.C. Wong, V.M. Haughton, and J.S. Hyde, "Functional magnetic resonance imaging of complex human movements", Neurology, vol. 43, no. 11, pp. 2311-2318, 1993.
[32] S.G. Kim, J. Ashe, K. Hendrich, J.M. Ellermann, H. Merkle, K. Uğurbil, and A.P. Georgopoulos, "Functional magnetic resonance imaging of motor cortex: hemispheric asymmetry and handedness", Science, vol. 261, no. 5121, pp. 615-617, 1993.
[33] X.D. Zhang, "Entropy for the Complexity of Physiological Signal Dynamics", Adv. Exp. Med. Biol., vol. 1028, pp. 39-53, 2017.
[34] A.M. Sabatini, "Analysis of postural sway using entropy measures of signal complexity", Med. Biol. Eng. Comput., vol. 38, no. 6, pp. 617-624, 2000.
[35] C.K. Rhea, T.A. Silver, S.L. Hong, J.H. Ryu, B.E. Studenka, C.M.L. Hughes, and J.M. Haddad, "Noise and complexity in human postural control: interpreting the different estimations of entropy", PLoS One, vol. 6, no. 3, p. e17696, 2011.
[36] P.C. Fino, A.R. Mojdehi, K. Adjerid, M. Habibi, T.E. Lockhart, and S.D. Ross, "Comparing postural stability entropy analyses to differentiate fallers and non-fallers", Ann. Biomed. Eng., vol. 44, no. 5, pp. 1636-1645, 2016.
[37] C. Chen, Y. Jin, I.L. Lo, H. Zhao, B. Sun, Q. Zhao, J. Zheng, and X.D. Zhang, "Complexity Change in Cardiovascular Disease", Int. J. Biol. Sci., vol. 13, no. 10, pp. 1320-1328, 2017.
[38] L. Montesinos, R. Castaldo, and L. Pecchia, "On the use of approximate entropy and sample entropy with centre of pressure time-series", J. Neuroeng. Rehabil., vol. 15, no. 1, p. 116, 2018.
[39] A. Mengarelli, F. Verdini, S. Cardarelli, A. Tigrini, A. Strazza, F.D. Nardo, R. Anna Rabini, O. Mercante, and S. Fioretti, "Complexity Measures of Postural Control in Type-2 Diabetic Subjects", Annu. Int. Conf. IEEE Eng. Med. Biol. Soc., vol. 2019, pp. 3527-3530, 2019.
[40] D.E. Lake, J.S. Richman, M.P. Griffin, and J.R. Moorman, "Sample entropy analysis of neonatal heart rate variability", Am. J. Physiol. Regul. Integr. Comp. Physiol., vol. 283, no. 3, pp. R789-R797, 2002.
[41] J.R. Moorman, J.B. Delos, A.A. Flower, H. Cao, B.P. Kovatchev, J.S. Richman, and D.E. Lake, "Cardiovascular oscillations at the bedside: early diagnosis of neonatal sepsis using heart rate characteristics monitoring", Physiol. Meas., vol. 32, no. 11, pp. 1821-1832, 2011.
[42] S.M. Pincus, I.M. Gladstone, and R.A. Ehrenkranz, "A regularity statistic for medical data analysis", J. Clin. Monit., vol. 7, no. 4, pp. 335-345, 1991.
[43] S. Pincus, "Approximate entropy (ApEn) as a complexity measure", Chaos, vol. 5, no. 1, pp. 110-117, 1995.
[44] J. S. Richman, and J. R. Moorman, "Physiological time-series analysis using approximate entropy and sample entropy", Am J Physiol Heart Circ Physiol, vol. 278, no. 6, pp. H2039-H2049, 2000.
[45] A. Delgado-Bonal, and A. Marshak, "Approximate Entropy and Sample Entropy: A Comprehensive Tutorial", Entropy (Basel), vol. 21, no. 6, p. 541, 2019.
[46] R.C. Oldfield, "The assessment and analysis of handedness: The Edinburgh inventory", Neuropsychologia, vol. 9, no. 1, pp. 97-113, 1971.
[47] L.A.R. Sacrey, J.M. Karl, and I.Q. Whishaw, "Development of visual and somatosensory attention of the reach-to-eat movement in human infants aged 6 to 12 months", Exp. Brain Res., vol. 223, no. 1, pp. 121-136, 2012.
[48] J.W. Flindall, and C.L.R. Gonzalez, "On the evolution of handedness: evidence for feeding biases", PLoS One, vol. 8, no. 11, p. e78967, 2013.
[49] C. Chen, K. Kreutz-Delgado, M.I. Sereno, and R.S. Huang, "Unraveling the spatiotemporal brain dynamics during a simulated reach-to-eat task", Neuroimage, vol. 185, pp. 58-71, 2019.
[50] N. Praditpod, Detectors for Early Detection of Movement Disorders.Master of Science.. School of Science and Engineering, University of Dundee: UK, 2017.
[51] E.M. Diaz, O. Heirich, M. Khider, and P. Robertson, "Optimal sampling frequency and bias error modeling for foot-mounted IMUs", International Conference on Indoor Positioning and Indoor Navigation, pp. 1-9, 2013.
[52] S.M. Pincus, "Approximate entropy as a measure of system complexity", Proc. Natl. Acad. Sci. USA, vol. 88, no. 6, pp. 2297-2301, 1991.
[53] S.M. Pincus, Quantifying Complexity and Regularity of Neurobiological Systems.Methods in Neurosciences., vol. Vol. 28. Academic Press, 1995, pp. 336-363.
[54] S.M. Pincus, T.R. Cummins, and G.G. Haddad, "Heart rate control in normal and aborted-SIDS infants", Am. J. Physiol., vol. 264, no. 3 Pt 2, pp. R638-R646, 1993.
[55] C. Tomkins-Lane, "An Introduction to Non-parametric Statistics for Health Scientists", Health Sci. J., vol. 3, no. 1, 2006.
[56] M.A. Pett, Nonparametric statistics for health care research: Statistics for small samples and unusual distributions.. Sage Publications, 2015.
[57] F.S. Nahm, "Nonparametric statistical tests for the continuous data: the basic concept and the practical use", Korean J. Anesthesiol., vol. 69, no. 1, pp. 8-14, 2016.
[58] H.B. Xie, W.X. He, and H. Liu, "Measuring time series regularity using nonlinear similarity-based sample entropy", Phys. Lett. A, vol. 372, no. 48, pp. 7140-7146, 2008.
[59] F. Kaffashi, R. Foglyano, C. G. Wilson, and K. A. Loparo, "The effect of time delay on Approximate & Sample Entropy calculations", Physica D: Nonlinear Phenomena, vol. 237, no. 23, pp. 3069-3074, 2008.
[60] H.T. Wu, C.C. Liu, M.T. Lo, P.C. Hsu, A.B. Liu, K.Y. Chang, and C.J. Tang, "Multiscale cross-approximate entropy analysis as a measure of complexity among the aged and diabetic", Comput. Math. Methods Med., vol. 2013, pp. 1-7, 2013.
[61] M.O. Sokunbi, G.G. Cameron, T.S. Ahearn, A.D. Murray, and R.T. Staff, "Fuzzy approximate entropy analysis of resting state fMRI signal complexity across the adult life span", Med. Eng. Phys., vol. 37, no. 11, pp. 1082-1090, 2015.
[62] C. Hansen, Q. Wei, J.S. Shieh, P. Fourcade, B. Isableu, and L. Majed, "Sample Entropy, Univariate, and Multivariate Multi-Scale Entropy in Comparison with Classical Postural Sway Parameters in Young Healthy Adults", Front. Hum. Neurosci., vol. 11, pp. 206-206, 2017.
[63] R.G. Carson, D. Goodman, R. Chua, and D. Elliott, "Asymmetries in the regulation of visually guided aiming", J. Mot. Behav., vol. 25, no. 1, pp. 21-32, 1993.
[64] J. Tretriluxana, S. Kantak, S. Tretriluxana, A.D. Wu, and B.E. Fisher, "Low frequency repetitive transcranial magnetic stimulation to the non-lesioned hemisphere improves paretic arm reach-to-grasp performance after chronic stroke", Disabil. Rehabil. Assist. Technol., vol. 8, no. 2, pp. 121-124, 2013.
[65] D.P. Carey, and J. Liddle, "Hemifield or hemispace: what accounts for the ipsilateral advantages in visually guided aiming?", Exp Brain Res, vol. 230, no. 3, pp. 323-331, 2013.
[66] J.E. Schaffer, and R.L. Sainburg, "Interlimb differences in coordination of unsupported reaching movements", Neuroscience, vol. 350, pp. 54-64, 2017.
[67] N. Runnarong, J. Tretriluxana, W. Waiyasil, P. Sittisupapong, and S. Tretriluxana, "Age-related changes in reach-to-grasp movements with partial visual occlusion", PLoS One, vol. 14, no. 8, p. e0221320, 2019.
[68] R.S. Woodworth, "Accuracy of voluntary movement", Psychological Review: Monograph Supplements, vol. 3, no. 3, p. i, 1899.
[69] L. B. Bagesteiro, and R. L. Sainburg, "Handedness: Dominant arm advantages in control of limb dynamics", J. Neurophysiol., vol. 88, no. 5, pp. 2408-2421, 2002.
[70] P.J. Bryden, and E.A. Roy, "A new method of administering the Grooved Pegboard Test: Performance as a function of handedness and sex", Brain Cogn., vol. 58, no. 3, pp. 258-268, 2005.
[71] T. Noguchi, S. Demura, Y. Nagasawa, and M. Uchiyama, "An examination of practice and laterality effects on the Purdue Pegboard and Moving Beans with Tweezers", Percept. Mot. Skills, vol. 102, no. 1, pp. 265-274, 2006.
[72] J. Mathew, F.R. Sarlegna, P-M. Bernier, and F.R. Danion, "Handedness matters for motor control but not for prediction", eNeuro, vol. 6, no. 3, 2019.
[73] T. Tajika, T. Kobayashi, A. Yamamoto, H. Shitara, T. Ichinose, D. Shimoyama, C. Okura, S. Kanazawa, A. Nagai, and K. Takagishi, "Relationship between grip, pinch strengths and anthropometric variables, types of pitch throwing among Japanese high school baseball pitchers", Asian J. Sports Med., vol. 6, no. 1, pp. e25330-e25330, 2015.
[74] D. Öcal Kaplan, "Evaluating the relation between dominant and non-dominant hand perimeters and handgrip strength of basketball, volleyball, badminton and handball athletes", Int J. Env. & Sci. Edu., 2016.
[75] J. Gao, J. Hu, and W.-W. Tung, "Entropy measures for biological signal analyses", Non-Linear Dynamics, vol. 68, pp. 431-444, 2012.
[76] J.M. Yentes, N. Hunt, K.K. Schmid, J.P. Kaipust, D. McGrath, and N. Stergiou, "The appropriate use of approximate entropy and sample entropy with short data sets", Ann. Biomed. Eng., vol. 41, no. 2, pp. 349-365, 2013.