RESEARCH ARTICLE
Patient-Specific Static Structural Analysis of Femur Bone of different lengths
K.N. Chethan1, Shyamasunder N. Bhat2, Mohammad Zuber1, Satish B. Shenoy*, 1
Article Information
Identifiers and Pagination:
Year: 2018Volume: 12
First Page: 108
Last Page: 114
Publisher ID: TOBEJ-12-108
DOI: 10.2174/1874120701812010108
Article History:
Received Date: 29/8/2018Revision Received Date: 06/12/2018
Acceptance Date: 10/12/2018
Electronic publication date: 31/12/2018
Collection year: 2018

open-access license: This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International Public License (CC-BY 4.0), a copy of which is available at: https://creativecommons.org/licenses/by/4.0/legalcode. This license permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Background:
The femur bone is an essential part of human activity, providing stability and support in carrying out our day to day activities. The inter-human anatomical variation and load bearing ability of humans of different heights will provide the necessary understanding of their functional ability.
Objective:
In this study, femur bone of two humans of different lengths (tall femur and short femur) were subjected to static structural loading conditions to evaluate their load-bearing abilities using Finite Element Analysis.
Methods:
The 3D models of femur bones were developed using MIMICS from the CT scans which were then subjected to static structural analysis by varying the load from 1000N to 8000N. The von Mises stress and deformation were captured to compare the performance of each of the femur bones.
Results:
The tall femur resulted in reduced Von-Mises stress and total deformation when compared to the short femur. However, the maximum principle stresses showed an increase with an increase in the bone length. In both the femurs, the maximum stresses were observed in the medullary region.
Conclusion:
When the applied load exceeds 10 times the body weight of the person, the tall femur model exceeded 134 MPa stress value. The short femur model failed at 9 times the body weight, indicating that the tall femur had higher load-bearing abilities.
1. INTRODUCTION
Bones are the vital organs in the human body, which give stability and strength. Human body consists of 270 bones
at birth and reduces to 206 bones in case of adults [1]. Hip joint being the second largest weight-bearing joint after knee, is one of the key joints which transmits the loads to lower abdomen during walking, standing, running, and/or stumbling [2]. This ball and socket type joint is supported by many well-balanced muscles [3]. The average length of femur bone varies from 42cm to 48cm in adults [4]. Hip joint consists of a femoral head, femur and lateral condyle. A typical healthy hip joint with its salient feature is shown in Fig. (1). Femoral head articulates into the acetabulum of pelvis [5]. It has six degrees of freedom namely flexion, extension, abduction, adduction, internal rotation and external rotation [6]. The hip joints give stability between the upper body and lower body and transmit the loads from upper body to lower body. The femoral head meshes with acetabulum and lateral condyle meshes with the tibia of knee joint [6]. The femur bone consists of the soft and spongy cancellous bone surrounded by the cortical bone which is harder, rigid. The centre of the femur is hollow which houses the bone marrow. The day to day activities such as walking, running exert force on the joint. Some studies have explored the effect of various activities on the hip joint [7, 8]. However, the effect of bone height and their load bearing ability is yet to be explored. Previously many studies have been carried out using Finite element methods to evaluate human activities [9-11].In the present study, a three-dimension patient-specific model of femur of different heights was analysed and evaluated for various forces acting on the hip joint.
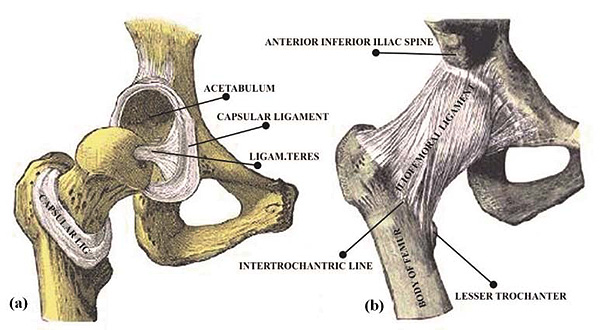 |
Fig. (1). The natural hip joint (right hip). (a) Capsule removed anterior aspect, (b) showing the ligament [6, 11-13]. |
2. MATERIALS AND METHODS
The study involves data from humans and Institutional ethical clearance was obtained from the Kasturba Medical College, Manipal. The CT scan data in the form of Digital Imaging and Communications in Medicine (DICOM) format consist of two-dimensional gray scaled images of a human femur [14]. Two anonymised CT scans were considered for this study with a slice thickness of 0.625 mm [15, 16]. The 2 patients considered in this study were of 36 years old and 42 years having recorded weight of 70 Kg and 78 Kg, respectively. The length of the two femurs considered was 461mm and 413mm, which will be referred to in this study for the sake of comparison as tall femur and short femur, respectively. It has been reported in the literature that the average femur length of adult Asian subject varies from 420 mm to 480 mm [4]. Static structural analysis was carried out using Ansys R 18 to determine the load at which bone failure may occur [17].
The imported CT scan images in MIMICS are segmented to identify the femur [18]. The 3 Matic software is used for smoothening and wrapping of the bone. The final 3D model of the femur was further developed using Catia V6. The static structural analysis was carried out in Ansys R [18-20]. A mesh dependency study was accomplished to determine the appropriate mesh size for the unstructured mesh developed. The mesh size was gradually reduced from 10 to 1 mm in accordance with an earlier study [21]. The variation of the stress developed for change in mesh size is graphically shown in Fig. (2a). It can be observed from Fig. (2a) that the stresses decrease drastically up to mesh size of 4. Beyond the mesh size 4, there is no major variation in stresses for subsequent mesh size. Therefore, a mesh element size of 5 mm was considered as the grid independent size and meshed model for the size is as shown in Fig. (2b). Thus, the taller bone with length of 461mm had 494,574 elements and shorter bone with length of 413mm had 428,681elements.
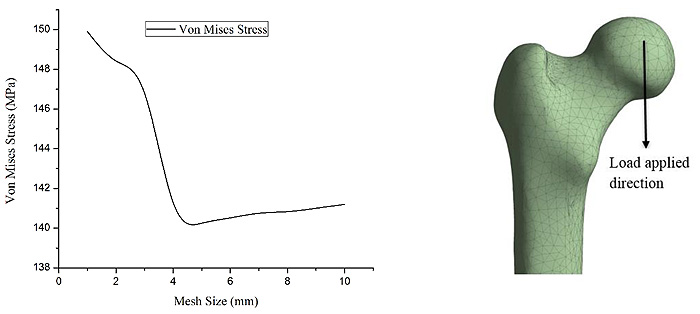 |
Fig. (2). (a) Variation of the stress values with a change in mesh size. (b) Femur after meshing. |
The material properties representing the femur are shown in Table 1. [6, 22, 23] For the analysis, the bone was considered as isotropic elastic material to minimise the complexity of the analysis.
| Sl | Material Properties | Cortical Bone |
|---|---|---|
| 1. | Young’s modulus | 17 GPa |
| 2. | Density | 2 g/cm3 |
| 3. | Poisson’s ratio | 0.30 |
| 4. | Tensile strength | 130MPa |
2.1. Boundary Conditions
Static structural analysis was carried out for both the models. The lateral condyle surface is fixed to mimic the normal human in all the analysis. Force applied varied from 1000N to 8000N and was applied on femoral head. The total deformation, von Mises stress and total deformation in Z axis and maximum principle stresses are evaluated. A maximum of 8000N was applied to both the models which is almost 10 times the body weight [24, 25]. Usually, in day to day activities maximum of 10 times of body weight is induced by the hip joint [26].
3. RESULTS & DISCUSSION
Bone is a rigid structure with harder at outer surface known as cortical bone and soft at inner surface known as cancellous bone. In the analysis, the bone was considered as the isotropic and static analysis was carried out to evaluate the stresses induced in the bone during different activities [21]. In this work, the CT scan images of 2 patients were modelled three dimensionally as complete solid femurs (tall femur and short femur) without considering separate properties for cortical, cancellous bone [27]. Figs. (3 and 4) provide the contour plots for deformation and von Mises stresses developed for tall femur and short femur respectively. It can be observed that both tall femur and short femur exhibit an identical pattern of results with varying load conditions. It can be found that the total deformation along the axis where the load is applied is lesser than the total deformation for both cases. In general, the stresses were predominantly induced in the medullary region of the femur and the distal end experienced lesser stress value. This is because it is fixed at the distal end, and the load applied was from the femoral head to mimic the actual conditions.
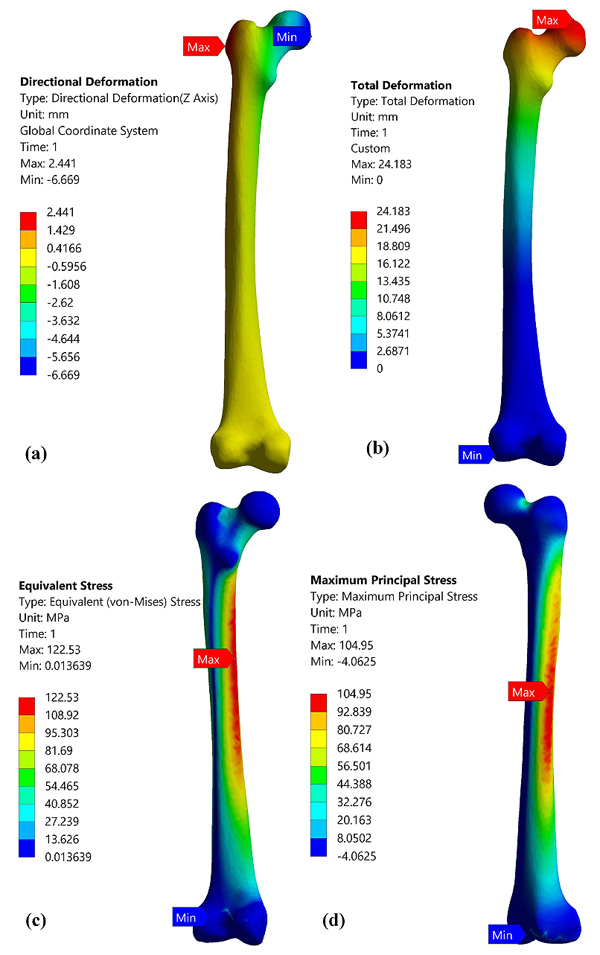 |
Fig. (3). Static analysis of tall femur of length 461mm under load 7000N force (a). Direction deformation, (b) Total deformation, (c) von Mises stress, (d) Maximum principle stress. |
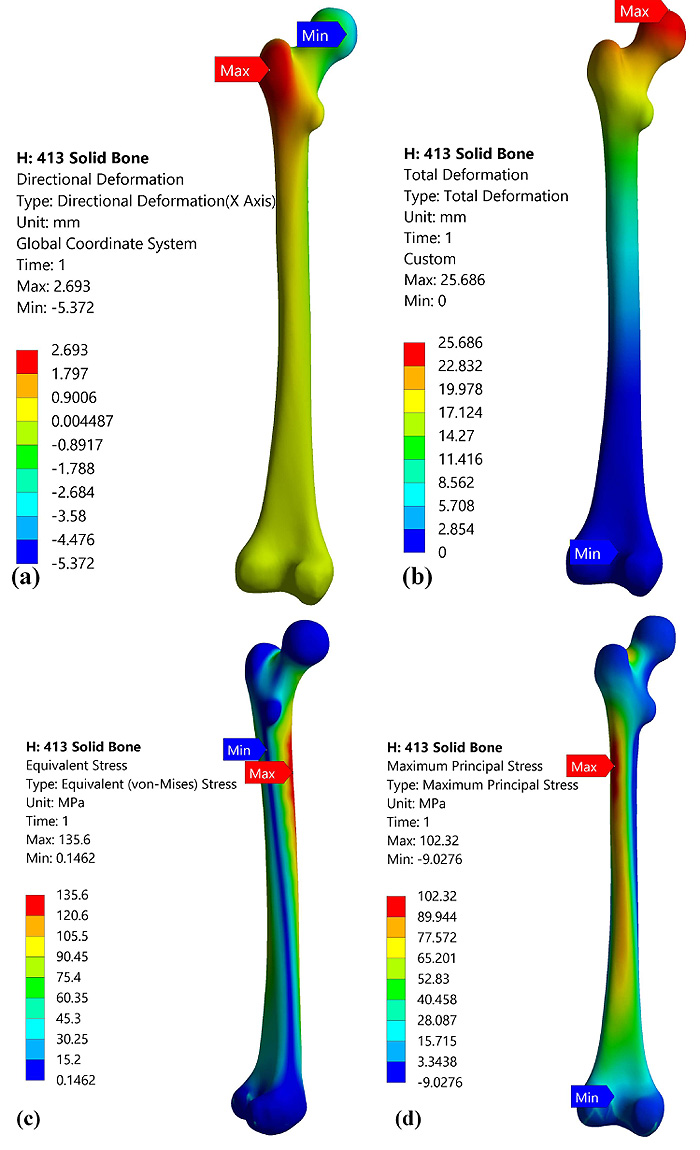 |
Fig. (4). Static analysis of short femur of length 413mm at load of 8000N force (a). Direction deformation, (b) Total deformation, (c) von Mises stress, (d) Maximum principle stress. |
When the loads were varied from 1000N to 8000N, a significant increase in the deformation and stress was observed as shown in Fig. (5). The tall femur model experienced less deformation along the load acting axis, when compared to the short femur. But with respect to maximum principle stresses the short femur model showcased lesser values compared to the tall femur. As the length of the femur bone increases it has lesser ability to withstand more loads and also the stability of the bone decreases. The von Mises stresses developed in the models increased with increase in the load. A femur bone can withstand maximum stress of 134 MPa in adults as per literature [28-30]. In the present study, the tall femur model could withstand more than 10 times the body weight with respect to patient weight. However, the von Mises stress exceeded more than 134 MPa when the load increased to more than 11 times the original body weight, indicating failure of the femur. The short femur having 431 mm length failed when the load was only 9 times the original body weight. In the case of short femur having a length of 413mm, the von Mises stresses were more than the fracture value predicted in literature when the load of 10 times the body weight was applied. This shows that the taller femur had significant load-bearing abilities. Thus, short patients who are obese would suffer from severe orthopedic issues [31, 32]. The study can be further performed by considering many samples with different age groups to clearly define the weight at which the femurs are safer with respect to the patient’s height. Also, by considering the muscles and tissues further clarity on the load carrying capacity of femur bone can be captured with regards to various activities.
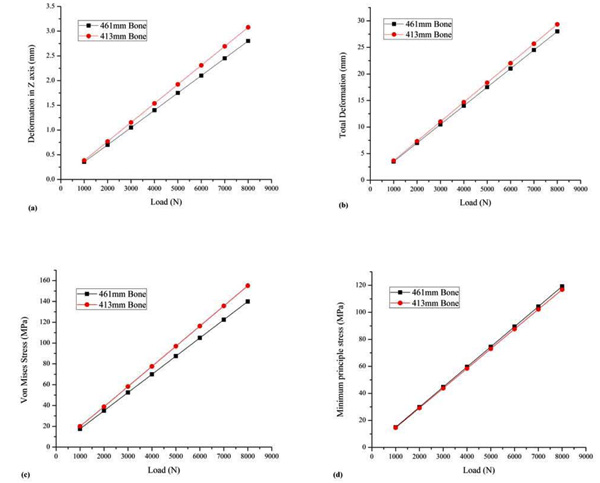 |
Fig. (5). (a) Deformation in Z-axis in mm; (b) Total deformation in mm; (c) von Mises Stress in MPa; (d) Maximum principle stress in MPa. |
CONCLUSION
The femur is a rigid and key organ which provides strength and stability for humans to perform various tasks. In this study, the CT scan data of a tall and a short patient were developed as a complete solid bone. The loads were varied from 1000N to 8000N up to 10 times the body weight and static analysis was carried out to determine the deformation and von Mises stress. It was observed that stresses in both the models were more at medullary region compared to the head and condyle part. It was shown that the load carrying capacity of femur increases with increase in the femur length. The tall femur model could withstand more than 10 times the body weight but the short femur having 431 mm length failed when the load was only 9 times the original body weight. So, it is clear that taller patients have reduced risk of femoral fracture. As the body weight increases, the load carrying capacity of femur reduces.
ETHICS APPROVAL AND CONSENT TO PARTICIPATE
The Ethical clearance is obtained by institutional ethical committee Kasturba Medical College and Hospitals.
HUMAN AND ANIMAL RIGHTS
No Animals were used in this research. All human research procedures followed were in accordance with the ethical standards of the committee responsible for human experimentation (institutional and national), and with the Helsinki Declaration of 1975, as revised in 2013.
CONSENT FOR PUBLICATION
Informed consent was obtained from all the participants.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
The authors thank Radiology department, Kasturba Medical College, Manipal for providing CT scan data of the patients to carry out this work.








