All published articles of this journal are available on ScienceDirect.
Alternating Periods of High and Low-Entropy Neural Ensemble Activity During Image Processing in the Primary Visual Cortex of Rats
Abstract
The response properties of individual neurons in the primary visual cortex (V1) are among the most thoroughly described in the mammalian central nervous system, but they reveal less about higher-order processes like visual perception. Neural activity is highly nonlinear and non-stationary over time, greatly complicating the relationships among the spatiotemporal characteristics of visual stimuli, local field potential (LFP) signal components, and the underlying neuronal activity patterns. We applied discrete wavelet transformation to detect new features of the LFP that may better describe the association between visual input and neural ensemble activity. The relative wavelet energy (RWE), wavelet entropy (WS), and the mean WS were computed from LFPs recorded in rat V1 during three distinct visual stimuli: low ambient light, a uniform grey computer screen, and simple pictures of common scenes. The time evolution of the RWE within the γ band (31-62.5 Hz) was the dominant component over certain periods during visual stimulation. Mean WS decreased with increasing complexity of the visual image, and the time-dependent WS alternated between periods of highly ordered and disordered population activity. In conclusion, these alternating periods of high and low WS may correspond to different aspects of visual processing, such as feature extraction and perception.
INTRODUCTION
A comprehensive description of the relationship between visual stimuli and neuronal population response patterns [1] that underlies visual encoding, processing, and perception is the fundamental goal of visual research [1-4]. The ability to derive meaning from complex sensory inputs requires the integration of information over space and time. Visual processing occurs at all levels of the visual pathway, but a primary focus historically has been the primary visual cortex (area V1) [2]. Neurons in V1 respond selectively to distinct visual inputs ranging in complexity from lines of a specific orientation to complete shapes [4]. Moreover, the position of V1 in occipital cortex allows for the analysis of information coding without interfering with purely optical aspects of visual function.
Local field potentials (LFPs) are low-frequency extracellular voltage fluctuations [5] that represent the sum of current sources and sink from postsynaptic potentials and action potentials originating in the vicinity of the microelectrode tip [6]. These field potentials can also reflect synchronized neuronal oscillations, at least within the low frequency range [7, 8]. In contrast to intracellular voltage recordings, LFP methods allow for stable multichannel recording from hundreds of sites to assess changes in the activity patterns and synchronization over large regions of V1. However, the collected responses include complex information of spatial distribution of current sources and sinks that are also filtered by the extracellular resistance. It is thus difficult to associate LFP waveforms with specific neural response patterns, particularly in neural structures without highly segregated synaptic inputs. Nonetheless, numerous studies have analyzed the associations among specific LFP components, visual inputs, and neuronal responses in primary visual cortex [9-12]. While the responses of individual V1 neurons to specific stimulus patterns in the receptive field are well described, it is still unclear how an ensemble of V1 neurons interacts to produce broad patterns of activity representing external visual stimuli changing in space and time. Oscillatory activities, which could be conveniently measured by LFP array recording, contain information carrying capacity of frequency codes [13-15].To understand how these oscillations are synchronized or desynchronized by external visual stimuli could be the first step to explore the visual sensory mechanism. The pattern could be analyzed by applying methods of system theory (e.g., Fourier-based methods [16] and chaos theory [17]) to LFP signals because changes in LFP activity occur in temporal relation to triggering events and correspond to transitions from disordered to ordered states (or vice versa).
Different methods have been proposed to quantify the complexity of brain activity synchronization [18, 19]. Spectral entropy is a measure of the distribution of the Fourier power spectrum of a signal in the frequency domain [20, 21] and can describe the characteristic LFP responses induced by visual stimuli. The multiscale entropy (MSE) was one of the most effective methods that explicitly accounts for multiple time scales inherent in complex electrophysiological data [22]. The scales are determined by the "coarse-grained" procedure, which essentially represents a linear smoothing and decimation of the original time series. MSE is finally computed by applying sample entropy (SampEn) [23]. However, these methods are not well adapted to nonlinear and nonstationary LFP signals. Many approaches were developed to solve the problem. One is to analyze spectra within short epochs, termed short-time Fourier transform (STFT), but this method cannot reveal the temporal evolution of complex LFP dynamics because reducing the time window degrades the range of the frequency resolution. This limitation becomes important when the signal has transient components localized in time, such as responses evoked by stimulation. Another method widely used to quantify the time evolution of nonlinear LFP dynamics is based on chaos theory (e.g., measurement of the correlation dimension and the largest Lyapunov exponent). Indeed, recent work shows that nonlinear relations between neural ensembles may not be detected by linear methods in certain cases [24]. Despite the fact that this approach is suitable for nonlinear dynamics analysis, a basic requirement for application is stationarity of the time series, which suggests that the time series represents a unique and stable attractor [25]. Moreover, many improved multivariate multiscale approaches (such as adaptive multiscale entropy, intrinsic mode entropy and variance entropy) were proposed to measure the complexity of the data over multiple adaptive scales that are intrinsically determined by multivariate empirical mode decomposition (MEMD) [26-28]. The results demonstrate that this method is able to reveal the underlying complex dynamics for nonlinear/nonstationary neural data. But the intrinsic mode functions (IMFs) decomposed by MEMD depend on adaptive scales of signal and the entropy of specific frequency components cannot be estimated.
Orthogonal discrete wavelet transform does not require signal stationarity [29]. Wavelet entropy (WS) is an ideal measure of the complexity of LFPs under different visual stimulus conditions. Furthermore, it can provide additional information about the underlying dynamic processes occurring within short LFP segments. The purpose of the study was to investigate the nonlinear dynamic properties of neural ensemble activity in the primary visual cortex of rats following differential visual stimuli. We analyzed the time-evolving entropy from wavelet transformation to reveal the dynamic changes in the frequency spectra and entropy (synchronization vs. desynchronization) in the V1 field potential array associated with visual stimuli of varying complexity. The relative wavelet energy (RWE), wavelet entropy (WS), and the mean RWE and WS were calculated to quantify LFP that will be used to describe the association between visual input and neural ensemble activity.
SUBJECTS AND METHODS
Animals and Surgery
Twenty adult Long-Evans rats, weighing 260 ± 20 g, were obtained from the Experimental Animal Center of Henan Province, China. The rats were housed under a 12 h/12 h light-dark cycle with room illumination at 200 lux. Experiments were approved by the Animal Care and Use Committee of Zhengzhou University and were performed in compliance with the guidelines of the National Institutes of Health for the Care and Use of Mammals in Neuroscience.
Prior to surgery, rats were anesthetized with 50 mg/ml ketamine (100 mg/kg), 20 mg/ml xylazine (5 mg/kg), and acepromazine (2.5 mg/kg), followed by a maintenance dose of ~0.2-0.3 ml total volume per hour. The maintenance dose was sufficient to keep the heart rate below 360 beats/min. Atropine (0.3 mg/kg) and dexamethasone (2 mg/kg) were administered subcutaneously to reduce secretions and edema, respectively. A small-animal monitoring system (MouseSTAT-CO2, KENT) was used to control body temperature and to continuously monitor heart rate (HR), oxyhemoglobin saturation, and perfusion index.
The animal was secured in a stereotaxic apparatus and body temperature maintained at 37°C-38°C as measured at the anus using a feedback-controlled heating pad. A craniotomy was made over area V1 contralateral to the open testing eye (coordinates: 0-4 mm anterior to lambda and 2.5-4.5 mm lateral to the midline; Paxinos and Watson 2009) [30]. The ipsilateral eye was covered during recordings. A microelectrode array (MEA, Microprobe 2×8 channel platinum-iridium array, intercontact distance 250 ìm) was positioned using a micromanipulator (MX7600, Siskiyou). Electrode impedance (0.50~1.0M) was measured in saline prior to implantation. The electrode tips penetrated to a depth of 360-600 ìm to capture activity from layer 4 [31]. The array was repositioned for a new recording session every ≈20 min. Signal-to-noise ratio was at least 2.5-3.0 as measured by the ratio of mean spike amplitude to mean peak-to-peak noise.
Data Collection and Visual Stimulation
Local field potential signals obtained by the MEA were recorded by a Cerebus 128-channel acquisition system (Blackrock Microsystems, Salt Lake, USA) at 30 kHz with 16-bit digitization. Signals were then converted to 2 kHz, low-pass filtered at 250 Hz (second-order Butterworth), notch filtered at 50 Hz, high-pass filtered (0.3 Hz) to remove baseline drift, and normalized using the z-score function.
Visual stimuli were generated by the Matlab toolbox and displayed on an LED monitor (10 inch, maximum luminance of 90 cd/m2, 1280 × 960 resolution) positioned 15 cm in front of the contralateral eye. The animal, monitor, and measurement system were shielded from room light using a cloth curtain. Receptive field locations for each microelectrode input in the contralateral visual field were first mapped with rear-projected light bars, and then the center and size of the aggregate area were determined so that multiple receptive fields could be simultaneously covered by the visual stimulus. The visual stimulation experiments were conducted to analyze the dynamic behavior of visual information processing in V1 during presentation of images of varying complexity, either ambient light matching that of the house conditions (200 lux), a gray screen of uniform luminance Fig. (1a), or one of the 20 stationary black and white images of simple scenes Figs. (1b,c). The average gray values of all the testing images were adjusted to maintain the same luminance for all the images. The pictures and grey screen were alternated and each presented for 1 s. Each test sequence was repeated 30 times, raw data of LFP from the 30 repeats were combined as the LFP of the experimental animal. Thus, two forms of activity were recorded from the open eye, low ambient light (200 lux) meant to replicate the typical eyes open state (with the monitor off) and the two visual stimuli from the monitor with all other ambient light sources shielded. Offline analysis was performed in Matlab.
Images used as visual stimuli: (a) uniform gray screen, (b, c) natural images.
Data Analysis
The wavelet transform can capture local temporal changes over a broad frequency spectrum, allowing for robust analysis of non-stationary and nonlinear LFPs with both detailed and coarse temporal features (e.g., sporadic, high frequency events and sustained, lower-frequency components) [32]. In the following section, we describe the outlines of the methodology. The relative wavelet energy (RWE), time-evolving WS, the mean RWE, and average wavelet entropy were obtained from these LFP array recordings.
(1) Wavelet Transform
Multiresolution discrete wavelet transform (DWT) has emerged as a popular tool for the analysis of complex physiological signals that vary in time and exhibit unique features at various frequencies or scales [33]. As with other wavelet transforms, a key advantage it has over Fourier transforms is temporal resolution: it captures both frequency and location in time information. The DWT of a signal x is calculated by passing it through a series of low-pass and high-pass filters. This decomposition has halved the time resolution since only half of each filter output characterises the signal. However, each output has half the frequency band of the input so the frequency resolution has been doubled. The wavelet coefficient γ of a signal x(t) with respect to mother wavelet ψ(t) is defined as:
 |
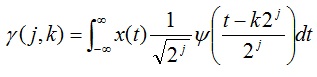(1) |
where j is the scale parameter and k is the shift parameter. For a wavelet centred at time zero and frequency f0, the wavelet coefficient γ(j, k) characterizes the signal x(t) around the time 2jk and frequency 2-jf0.
In order to capture the temporal evolution, the LFP is divided into a number of segments using a sliding temporal window. Let x = {x(i); i = 1, 2, …..N} denote the LFP signal. A sliding temporal window w ≤ N and a sliding interval Ä ≤ w are defined. The mth segment of LFP is defined as
 |
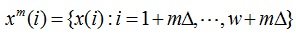(2) |
Where the maximum value of m is the integer part of (N – w + 1)/ Ä. Wavelet multiresolution decomposition was used for decomposing the signals in scale levels defined by the traditional cortical frequency bands on the electroencephalograph (a, b, ã, etc.). After eight-octave wavelet decomposition, the components of the following bands were obtained: 500-1000 Hz, 250-500 Hz, 125-250 Hz, 62.5-125 Hz (ã2), 31-62.5 Hz (ã), 15.5-31 Hz (b), 7.8-15.5 Hz (a), 3.9-7.8 Hz (è), and the remainder from 0.3-3.9 Hz corresponding to the ä band.
(2) Wavelet Entropy
For the mth segment of the LFP, the signal xm(i) is decomposed over j levels by DWT, and its energy at resolution level j and sample k is given by the square of the corresponding wavelet coefficients cjm, as defined by Equation(3):
 |
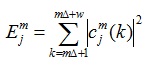(3) |
The total wavelet energy of the mth segment for all scales will be as follows:
 |
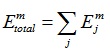(4) |
The relative wavelet energy (RWE) over scale j is defined by Equation (5):
 |
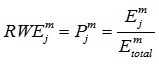(5) |
Clearly, for each time window m,
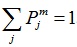, the distribution {Pjm} can be considered a time-scale density. The time-varying WS of signal xm is given by Equation (6),
 |
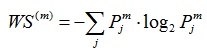(6) |
The WS reflects the time evolution of the degree of order/disorder of the signal, so it can provide useful information about the underlying dynamic processes associated with the signal [34].
The sliding window size was chosen empirically. We first calculated the WS for a 1-s segment of the actual LFP raw signal Fig. (2a), starting with w = 0.01 s and increased the duration in 0.01 s increments up to w = 0.3 s. The effects of window size are demonstrated in Fig. (2b). Wavelet entropy approaches a steady-state value for window sizes > 100 ms. Thus, w > 100 ms provides an unbiased estimate of entropy.
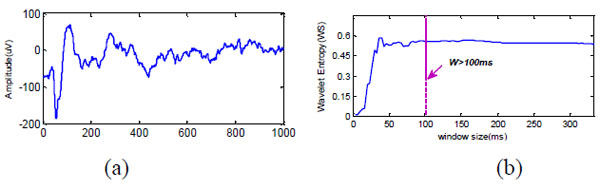
Effects of window size on the WS. (a) One second of actual LFP signal during stimulus presentation was chosen to find the optimal window size for evaluating the time-dependent WS. (b) Resulting WS plot versus window size. The plots indicate that w > 100 ms is appropriate for avoiding bias.
In order to obtain a quantifier for the whole time period under analysis, the mean RWE and temporal average of wavelet entropy (mean wavelet entropy) [35, 36] are defined respectively as:
 |
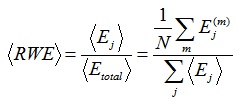(7) |
 |
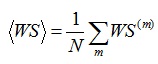(8) |
where N is the number of segments of the analyzed signal. The relative wavelet energy (RWE), wavelet entropy (WS), and the mean RWE and WS were analyzed with Matlab program (MathWorks, Natick, MA, USA).
(3) Statistics Analysis
The mean wavelet entropies of the recorded unit activities in area V1 were acquired for the three stimulus conditions. All WS values are expressed as mean ± SEM. All variables were tested for normality by the One-Sample Kolmogorov-Smirnov test and singular values were eliminated by outlier analysis.
Differences in mean WS values were tested by one-way ANOVA followed by post hoc pair-wise comparisons using Fisher’s test of least significant difference (LSD). A probability value of less than 0.01 was considered statistically significant. Data analysis was implemented in the Matlab development environment using both built-in functions and functions developed in-house.
RESULTS
Local field potentials were recorded in response to repeated visual inputs of three types: low ambient light (200 lux) within the curtain-shielded experimental system (referred to as the eyes open state), a uniform gray screen, and simple stationary images of common scenes (the latter two image types projected from an LCD monitor with no other ambient light). The dynamic properties of the multichannel LFP from V1 in response to the three visual input types were analyzed by DWT. In each trial, a moving window was applied to the LFP of every channel for one second after stimulus onset. The sliding window length w is 100 ms with a step of 50 ms.
Time-Evolving Wavelet Energy and Entropy
The time-varying RWE and WS values are useful measures of frequency spectrum variability over time and across channels [37]. Fig. (3a) shows the time series of LFP signals evoked by the three stimulus types from one channel. Both the uniform screen and stationary images evoked a negative deflection of the LFP response at around 100 ms after stimulus onset. The LFP oscillations evoked by the pictures had a marked slow negative wave with nadir between 500−700 ms. Note that LFP response patterns evoked by the two stable visual inputs (uniform grey background and pictures) share certain similarities and are distinct from the response in the eyes open state. The time evolution of the RWE for the major frequency bands (including ä, è, a, b,ã, and ã2) and corresponding temporal evolution of the total WS are displayed in Fig. (3b, c). For the eyes open condition, the corresponding RWE distribution Fig. (3), top of middle column) concentrates in lower frequency components (mainly below 30 Hz). However, the RWE of the ã band (31-62.5 Hz) is much higher in response to pictures, at least during certain periods of image presentation, and shows semi-periodic fluctuations. Thus, the ã frequency band may contribute to visual processing and perception. The wavelet entropy also showed time related changed (Fig. 3, right) during the stationary visual stimuli, indicating alternating periods of disorder and order, possibly corresponding to different phases of visual processing.
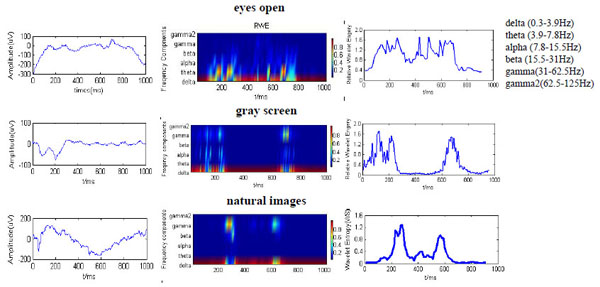
Dynamic properties of LFPs from V1 in response to low ambient light mimicking the typical eyes open state (top row), a uniform screen (middle row), or stationary images of typical scenes (natural images, bottom row). (a) Representative of one original LFP data. (b) Relative wavelet energy at six frequency channel in different times were illustrated by different color (Red for higher RWE, blue for lower RWE). (c) Change of WS during the data collection time window.
Mean RWE and Mean Wavelet Entropy
The mean RWE value for the entire one-second image presentation period provides information about the relative mean energy associated with each frequency band in the LFP signal, while RWE values over specific spans (100-300 ms, 500-800 ms) provide course descriptions of the timing of these energy peaks. In addition, they also give information about the microstates of order and disorder (or more complex order) present in the signal. To quantify the energy distribution for the whole time period, and to show how wavelet entropy changes under different conditions, we calculated mean RWEs of the major frequency bands ä (0.3-3.9 Hz), è (3.9-7.8 Hz), a (7.8-15.5 Hz), b (15.5-31 Hz), ã (31-62.5 Hz) and ã2 (62.5-125 Hz) (Table 1).
Mean relative wavelet energy (RWE) and mean wavelet entropy (WS) over the entire image presentation and within early and late segments.
| Epoch | Mean RWE | Mean WS | ||||||
| δ | θ | α | β | γ | γ2 | |||
| Eyesopen | 0-1s | 0.733 | 0.131 | 0.059 | 0.026 | 0.045 | 0.006 | 0.868 |
| 100-300 ms | 0.619 | 0.223 | 0.072 | 0.018 | 0.061 | 0.007 | 1.180 | |
| 500-800 ms | 0.847 | 0.039 | 0.046 | 0.034 | 0.029 | 0.005 | 0.739 | |
| Grayscreen | 0-1 s | 0.838 | 0.103 | 0.005 | 0.013 | 0.036 | 0.005 | 0.611 |
| 100-300 ms | 0.764 | 0.159 | 0.006 | 0.011 | 0.052 | 0.007 | 0.812 | |
| 500-800 ms | 0.912 | 0.047 | 0.004 | 0.015 | 0.020 | 0.003 | 0.372 | |
| Natural images | 0-1 s | 0.914 | 0.006 | 0.005 | 0.003 | 0.070 | 0.002 | 0.354 |
| 100-300 ms | 0.876 | 0.011 | 0.060 | 0.003 | 0.137 | 0.003 | 0.486 | |
| 500-800 ms | 0.952 | 0.005 | 0.003 | 0.004 | 0.035 | 0.001 | 0.202 | |
In the eyes open condition, the RWE of the ã band was minimal relative to RWEs of lower frequency bands (< 30 Hz). The mean wavelet entropy values remained relatively high (about 0.878), suggesting a disordered or highly complex ordered state. In response to image presentation, the ã component energy increased markedly (Fig. 3, middle column) within the periods 100-300 ms and 500-800 ms during figure presentation but was minimal between these periods. In response to the simple picture, a large burst of ä energy (above 90%) and two major periods of high ã energy (within the 100-300 ms and 500-800 ms segments) appeared during decreased mean RWE of the è and a components (Table 1).
These data reveal basic differences in the energy distribution of LFPs between the three visual stimulus conditions. In contrast to the eyes open condition, the neural activity in V1 during picture presentation shifted between high entropy (a disordered or more complex state) and low entropy (a more ordered state with corresponding lower mean entropy values). The mean wavelet entropy value was lower in response to the pictures compared to the uniform screen (0.354 vs. 0.611), indicating that more complex images are associated with a more ordered state.
Distinction of Dynamical Features in Different Conditions
To examine the general behavior of LFP signals in response to the three visual inputs, we evaluated mean wavelet entropies over the entire 1 s stimulus duration for different electrodes in the twenty LE rats. Excluding nonresponsive electrodes and those with poor signal-to-noise, 263 recordings were obtained during presentation of the three stimulus types and the mean wavelet entropies calculated. -The mean wavelet entropy value was significantly lower during presentation of the simple image compared to both the eyes open state and the gray screen presentation (Table 2). Thus, there was an inverse relationship between mean WS and image complexity, indicating that the neuronal response to simple images is characterized by alternating periods of order and disorder in V1. During the higher entropy periods, neurons in V1 may be processing a large amount of information, while the intervening periods of order may correspond to an integration process associated with perception.
DISCUSSION
Multichannel local field potentials from rat primary visual cortex evoked by inputs of varying complexity were analyzed by the orthogonal discrete wavelet transform method to derive quantitative parameters of visual processing dynamics in large neural populations. The principle parameters, the time-evolving RWE and WS, revealed clear differences in the processing dynamics of ambient light, uniform backgrounds, and stationary pictures. In general, images conducive to perception (pictures) evoked dynamic LFPs with alternating periods of low and high entropy, possibly reflecting periods of neuronal asynchrony associated with individual feature extraction and more ordered activity associated with integration (perception and recognition).
The WS has many advantages over other parameters for describing complex firing activity in neuronal populations. First, in contrast to spectral entropy, WS is capable of detecting changes in a nonstationary signal due to the localization characteristics of the wavelet transform. Second, the computational time required to acquire the time-evolving dynamic characteristics is shorter. Finally, noise contamination can be easily eliminated if concentrated in specific frequency bands.
There were significant differences in the time-evolving WS between the three forms of visual input studied, reflecting the distinct neuronal response patterns evoked. In the eyes open condition, neuronal activity in V1 was disordered or of high-order complexity as evidenced by the rapid fluctuations in the time-evolving WS. In contrast, stimulation with simple pictures was associated with alternating periods of high and low WS, indicating that visual processing involves periods of ordered (synchronized) and disordered (or complexly ordered) activity in V1. We suggest that the periods of disorder correspond to visual processing, while ordered activity may correspond to recognition. Furthermore, the RWE indicated that image processing is associated with the emergence of gamma frequency oscillations, an EEG component that has been linked to specific cognitive tasks [38, 39] such as visual discrimination [40].
The mean wavelet entropy provided general information on the degree of order/disorder or complexity/regularity associated with the LPF responses during processing of the visual stimulus, and clearly distinguished the three different stimulus types. There was an inverse relationship between the mean wavelet entropy of the V1 neural response and visual complexity, possibly reflecting the dominance of processing over recognition/perception under conditions of high visual information load. In the eyes open condition, the alpha wave component was depressed and the mean wavelet entropy was higher due to the disorder in cortical activity. Under conditions where image construction and perception are induced, as during presentation of a simple picture, there was an obvious increase in the gamma frequency band and a reduction in mean wavelet entropy. Phase-locking of oscillations between cortical areas may provide a mechanism for the transient formation of large distributed neuronal assemblies for higher level visual analysis [41]. For example, selective attention, visual feature extraction, binding of visual information, and recognition may involve synchronization of neuronal populations within multiple cortico cortical and cortical-hippocampal networks, consistent with our proposal that visual perception occurs during periods of lower wavelet entropy and higher ã band power in V1.
As for the limitation, since the rats were anesthetized during the measurements there is a possibility that change detection was not exactly due to the perception or feature extraction. However the animal was kept in a superfacial anesthesia status, as described previously [42]. Also, our results from multiple animals and multiple repeats demonstrated clear regulated pattern of WS. Therefore, we would speculate that the observed changes reflected response- specific visual cue instead of epiphenomenon. Given the large number of neurons involved in the visual image processing and the complexity of the response even at the single neuron level, it is difficult to establish precise correlations between neural activity patterns and visual cognitive tasks. However, the parameters RWE and WS quantify certain high-level characteristics of neural population activity and so may help decipher the complex encoding rules that underlie visual processing and object recognition. Future studies using these analytic methods on visually dominant species such as macaque monkeys are warranted.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
Declared none.
