All published articles of this journal are available on ScienceDirect.
Injury Risk Assessment of Non-Lethal Projectile Head Impacts
Abstract
Kinetic energy non-lethal projectiles are used to impart sufficient effect onto a person in order to deter uncivil or hazardous behavior with a low probability of permanent injury. Since their first use, real cases indicate that the injuries inflicted by such projectiles may be irreversible and sometimes lead to death, especially for the head impacts. Given the high velocities and the low masses involved in such impacts, the assessment approaches proposed in automotive crash tests and sports may not be appropriate. Therefore, there is a need of a specific approach to assess the lethality of these projectiles. In this framework, some recent research data referred in this article as “force wall approach” suggest the use of three lesional thresholds (unconsciousness, meningeal damages and bone damages) that depend on the intracranial pressure. Three corresponding critical impact forces are determined for a reference projectile. Based on the principle that equal rigid wall maximal impact forces will produce equal damage on the head, these limits can be determined for any other projectile. In order to validate the consistence of this innovative method, it is necessary to compare the results with other existing assessment methods. This paper proposes a comparison between the “force wall approach” and two different head models. The first one is a numerical model (Strasbourg University Finite Element Head Model-SUFEHM) from Strasbourg University; the second one is a mechanical surrogate (Ballistics Load Sensing Headform-BLSH) from Biokinetics.
1. INTRODUCTION
Kinetic energy non-lethal projectiles are used to impart sufficient effect onto a person in order to deter uncivil or hazardous behavior with a low probability of permanent injury. Since their first use, real cases indicate that the injuries inflicted by such projectiles may be irreversible and sometimes lead to death. The nature and severity of injuries resulting from their use depend, among others, on the impacted body part. Due to the phenomenon of ballistic dispersion, more vulnerable parts, like the head, may be unintentionally hit.
While the reported number of non-lethal projectile impacts to the head may be less compared to the other vital body parts, more serious injuries have been attributed to the head impacts [1]. Therefore, there is a necessity to assess the head impacts in order to allow a safer use of non-lethal projectiles. The goal is to define an employment doctrine for the non-lethal weapons in terms of shooting distances by predicting the lesions that can be inflicted by such weapons.
In this field, no standard exists and there is a lack of injury data, particularly on Post Mortem Human Subjects (PMHS). The only real data available in literature on this subject concern the work of Raymond from Wayne state University [2]. However, for ethical, legal, technical and financial considerations, tests on PMHS are difficultly feasible or even forbidden. Another source of information is DGA (Direction Générale de l’Armement, French Ministry of Defence) [3]. The approach developed at DGA (force wall approach) led to the definition of a simple experimental method based on shooting the projectile onto a rigid wall. Then, the force signal during this impact is measured in order to determine the maximum impact force on the head and the injury risk for such impact. So far, no study has been achieved to verify the relevance of the obtained results. This paper proposes a comparison between the results of the force wall approach and those obtained using two different head models.
The first one is a numerical model, the Strasbourg University Finite Element Head Model (SUFEHM) from Strasbourg University. The second model is a mechanical surrogate, the Ballistics Load Sensing Headform (BLSH), from Biokinetics and Associates, Ltd.
The current study is carried out using the FN303 non-lethal projectile from FN Herstal. Firstly, the experimental setups used for the force wall approach and the BLSH tests are presented. Secondly, the different numerical models are presented. Thirdly, the comparison between the results of the different methods and the discussions are presented. Finally, some remarks and suggestions conclude the article.
2. EXPERIMENTAL SETUPS
2.1. The Force Wall Approach
Since several years, the DGA, in partnership with engineers and medical experts in France, have undertaken a major research project in order to understand and explain blunt-impact injuries, especially the effects of non-lethal projectiles on the human body [3]. Its purpose is to implement a new method that allows an easy assessment of the critical injury and to propose lethality thresholds for these projectiles using measurable physical parameters. A substantial number of tests has been conducted on the head for a specific 40mm diameter benchmark projectile, the XM1006 shown in Fig. (1) [3].

Benchmark projectile XM1006.
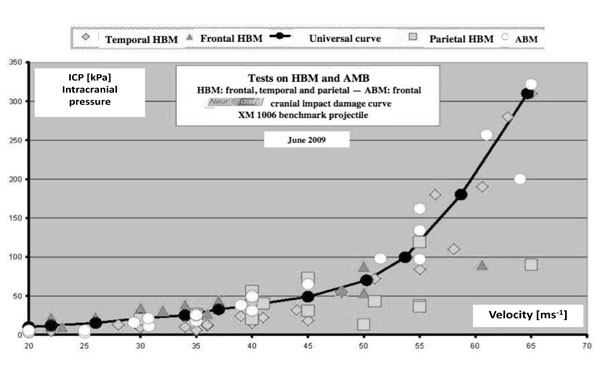
XM1006 head ICP curve [3].
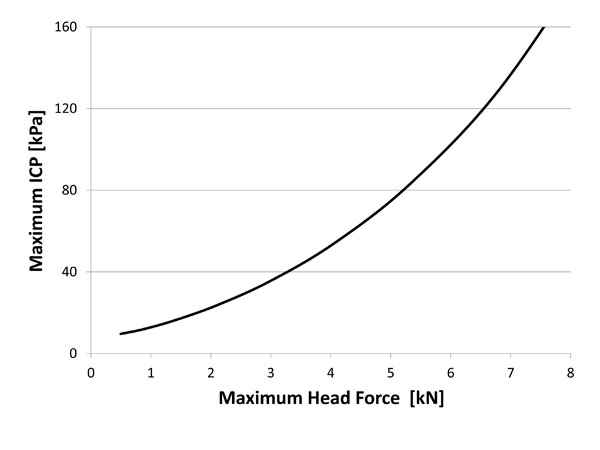
ICP and head force relation curve [3].

Rigid wall experimental setup.

Ballistics load sensing headform.
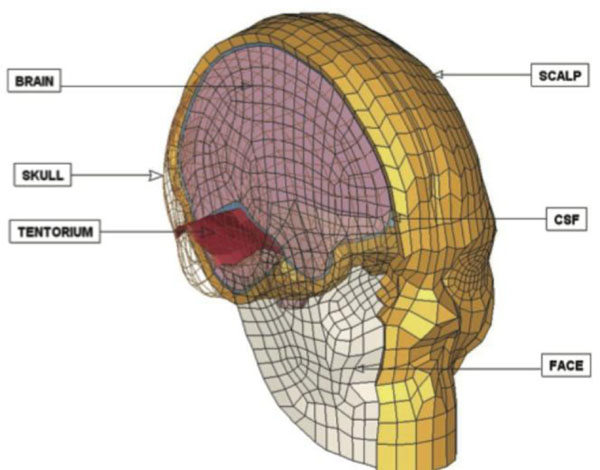
Strasbourg University Finite Element Head Model (SUFEHM).

FN303 projectile.
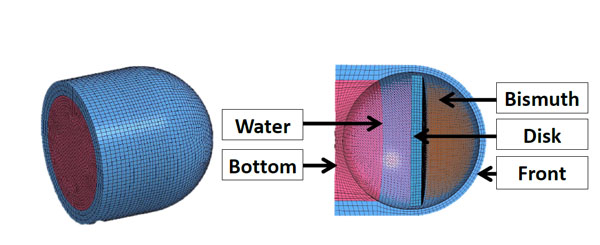
FN303 projectile finite element model.
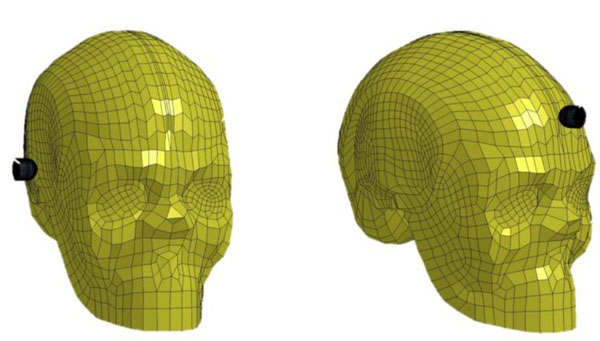
SUFEHM impact configurations- Left: temporal- Right: frontal.
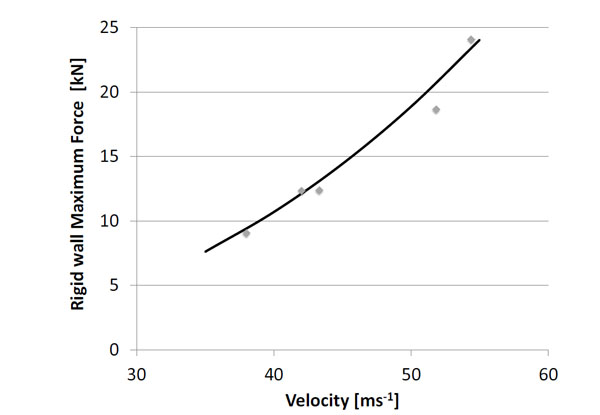
XM1006 rigid wall maximum force.
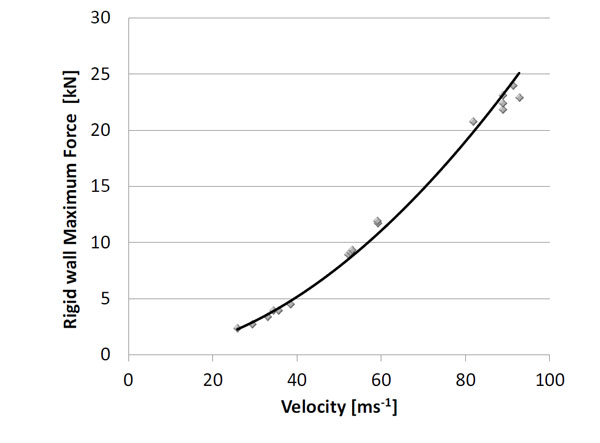
FN303 rigid wall maximum force.
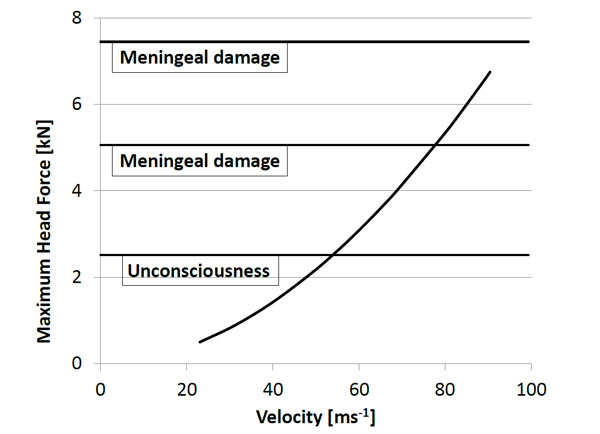
FN303 maximum head force curve.
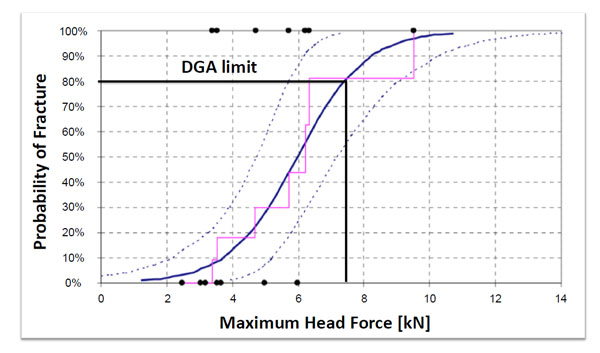
Injury risk function for the prediction of skull fracture based on the maximum force [2].
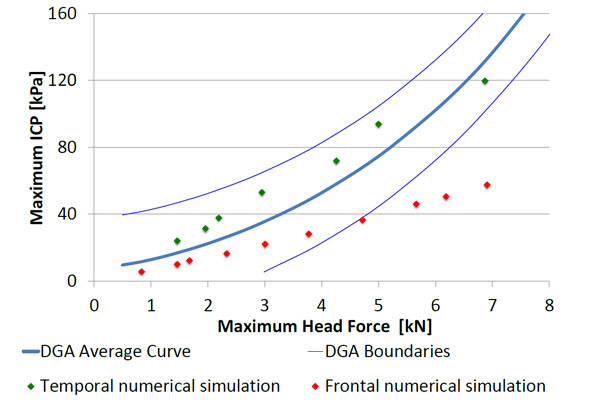
Comparison between the SUFEHM and the DGA ICP curve.
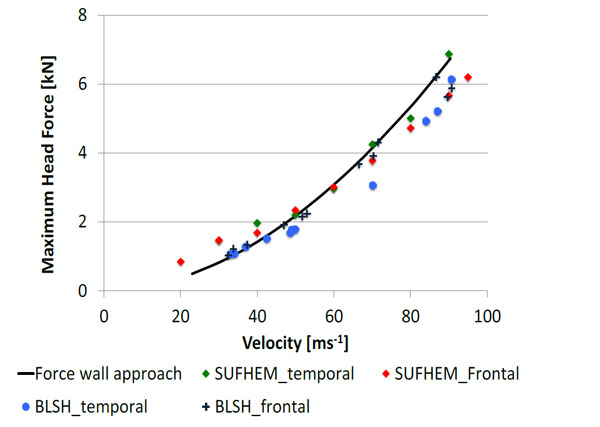
Comparison of the maximum forces between the SUFEHM, the BLSH and the force wall approach.
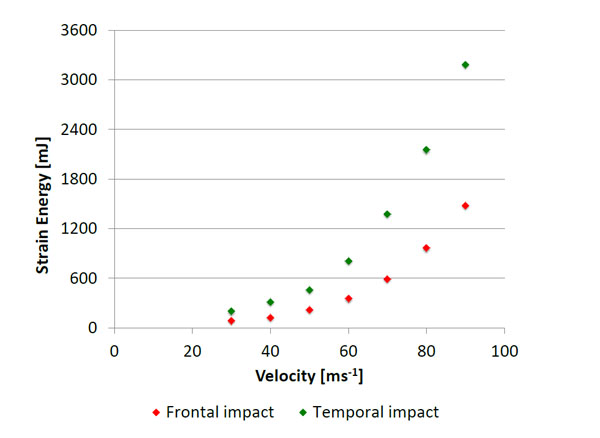
Evolution of the strain energy in the SUFEHM against the impact velocity.
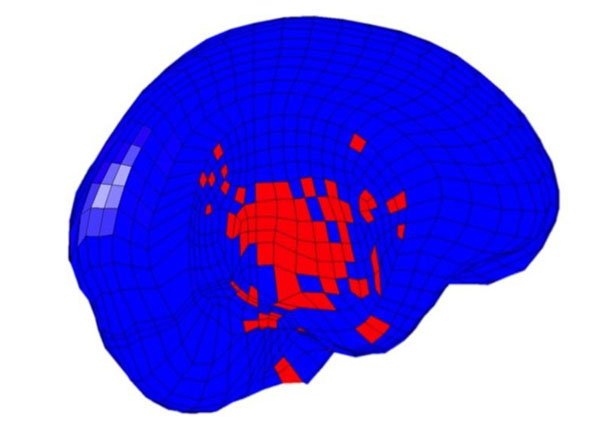
Example of fracture predicted by the SUFEHM for a temporal impact.
The first step of the study was to define a physiological benchmark parameter for cranial impact damage. Based on head protection impacts on Human Biological Models (HBM) and Animal Biological Models (ABM), the Intracranial Pressure (ICP) has been correlated to head injuries. The role of the ICP in the head damage has already been demonstrated in previous studies, for other types of impacts [4]. The ICP is measured on cisterna magna, relatively near the cerebellum [3]. The head damage curve linking the maximum ICP to the impact velocity for the XM1006 was determined using the different impact data on the temporal, frontal and parietal head parts for the low velocities. Only the temporal impacts are considered for the high velocities according to the worst case scenario approach (Fig. 2) [3]. The clinical findings on HBM and ABM allowed defining the damage threshold values presented in Table 1 [5]. Then, through numerical simulations, the relation between ICP and maximum impact force was derived (Fig. 3). This relation is supposed to be the same for any projectile impact [3]. Equation (1) gives the relation between maximum impact force on the head and impact velocity. This relation is obtained by combining the data from Fig. (2) and Fig. (3).
DGA head damage thresholds [3].
| Type of damage | Maximum ICP [kPa] | Maximum Head Force [kN] |
|---|---|---|
| Insignificant | P < 25 | F < 2.5 |
| Unconsciousness | 25 ≤ P < 45 | 2.5 ≤ F < 5.0 |
| Meningeal | 45 ≤ P < 150 | 5.0 ≤ F < 7.5 |
| Skull fracture | P ≥ 150 | F ≥ 7.5 |
SUFEHM tolerance limits for 50% risk of injury [11, 14].
| Injury | Criteria | Tolerance limit |
|---|---|---|
| Severe DAI | Brain Von Mises stress [kPa] | 53 |
| Mild DAI | Brain Von Mises stress [kPa] | 28 |
| Subdural hematoma | CSF strain energy [mJ] | 4950 |
| Skull fracture | Skull strain energy [mJ] | 865 |
FN303 projectile finite elements model properties.
| Solid Parts | ||||||||
|---|---|---|---|---|---|---|---|---|
| Density [kg/m3] | Young Modulus [MPa] | Poisson Coefficient | Mechanical Behavior | |||||
| Front | 8.1 10-2 | 5500 | 0.300 | Elastic | ||||
| Bottom | 8.1 10-2 | 5500 | 0.300 | Elastic | ||||
| Disk | 5460 | 5500 | 0,300 | Elastic | ||||
| SPH parts | ||||||||
| Density [kg/m3] | Mass of one particle [g] | Number of particles | Distance between particles [mm] | Mechanical Behavior | ||||
| Water | 1000 | 1.359 10-5 | 59380 | 0.239 | EOS Linear (C1= 2.2 10+3 MPa) |
|||
| Bismuth | 9790 | 1.115 10-4 | 56551 | 0.225 | EOS Linear (C1= 3.1 10+4 MPa) |
|||
Results of power curve parameters and dispersion corresponding to the rigid wall tests.
| Projectile | K | N | σ [kN] |
|---|---|---|---|
| XM1006 | 0.314 | 2.543 | 1.037 |
| FN303 | 0.381 | 1.882 | 0.846 |
(FXM)head = 0.083 (VXM / 10) 2.585 (1)
With
(FXM)head: maximum force of the XM1006 projectile on the head [kN].
VXM: impact velocity of the XM1006 projectile [ms-1].
The second step was to propose the force wall approach as method to easily assess any projectile using the XM1006 results on the head. This approach is based on shooting the projectile onto a rigid wall equipped with a piezoelectric force sensor. The wall is supposed to be infinitely rigid comparing to the projectiles.
The assumption is that: “two different projectiles producing the same maximum forces on the rigid wall will cause equivalent lesional effects on the head” [3].
Therefore, for a given projectile Y, shots on a rigid wall are performed at different velocities. A proposed relation between maximum force on rigid wall and impact velocity is given by equation (2).
FY = KY (VY / 10) NY (2)
With
FY: maximum force of projectile Y on rigid wall [kN].
VY: impact velocity of projectile Y [ms-1].
KY, NY: projectile Y power-law model parameters.
The same relation can be obtained for the XM1006 on the rigid wall as shown in equation (3).
FXM = KXM (VXM / 10) NXM (3)
With
FXM: maximum force of the projectile XM1006 on the rigid wall [kN].
VXM: impact velocity of projectile XM1006 [ms-1].
KXM, NXM: projectile XM1006 power-law model parameters.
The experimental setup for the rigid wall force measurement is shown in Fig. (4). The setup includes a pneumatic launcher, a structure considered sufficiently rigid (in comparison with the tested projectile) and equipped with a piezoelectric dynamic sensor Kistler 9061A, a high-speed camera and light spots. The impact force signal acquisition is carried out with a sample rate of 1 MHz and a 2x105 measuring points (samples), whereas the frame rate for the camera acquisition is 50 000 images/s. More details about the setup can be found in previous studies [5-7].
The force wall approach is used as follow: at the same force value for rigid wall impact, the relation between Vy and VXM is obtained from equation (2) and equation (3). Knowing the damage characteristics on the head for the XM1006, the corresponding Vy at the same head force value can be deduced from equation (1). The head force for the new projectile Y can now be found and the critical velocities can be calculated from the thresholds shown in Table 1.
2.2. The Mechanical Surrogate
The head mechanical surrogate used in the current study is the BLSH developed at Biokinetics and Associates, Ltd (Fig. 5). The BLSH enables a direct measurement of the dynamic loads imparted to the skull due to non-penetrating projectiles impacts. The BLSH is equipped with seven Kistler cells in order to measure the contact force. It allows assessing the temporal (two sides) and frontal impacts. The skull substructure is made of magnesium [2, 8]. A silicon rubber pad is used as a skin surrogate to cover the load cell array. This BLSH was originally developed to evaluate the risk of skull fracture caused by back face deformation of military helmets undergoing bullet impacts (Behind Armour Blunt Trauma). Raymond compared the forces measured on PMHS and those measured with the BLSH and other surrogates and concluded that the BLSH is the most suitable one for evaluating non-lethal projectile head impacts [2].
In the current study the BLSH is used to measure the impact force of the FN303. Two different headforms that correspond to the temporal and frontal impacts, respectively, are used. The experimental setup involved in this test is similar to the setup shown in Fig. (4). The rigid wall is replaced by the BLSH.
3. THE NUMERICAL MODEL
3.1. The SUFEHM
The numerical head model used for this study, shown in Fig. (6), is the SUFEHM developed by Kang et al. and represents a 50 percentile adult human head [9]. The model components are: skull, face, falx, tentorium, Cerebro-Spinal Fluid (CSF), scalp and brain (cerebrum-cerebellum-brainstem). The finite element mesh is continuous. SUFEHM consists of 13208 elements and its total mass is 4.7 kg [10]. The model is to be used with the LS-DYNA software.
Material properties of the CSF, scalp, facial bones, tentorium and falx are all isotropic, homogenous and elastic [10]. The brain is assumed to be viscoelastic [11]. The shear relaxation behaviour is described with equation (4).
G (t) =G∞ + (G0 - G∞) e-βt (4)
With
G0 short-time shear modulus.
G∞ long-time shear modulus.
β decay constant.
t time variable.
The skull material has three failure criteria expressions for four different types of in-plane damage mechanisms. Each of them predicts failure of one or more plies in a laminate. The longitudinal and transverse compressive and tensile strengths are respectively: 90 MPa for cortical bone and 34.8 MPa for diploe bone, with a shear stress parameter defined at -0.5 [10].
The model is validated according to three different experimental tests based on brain and skull biomechanical responses. The force contact validation on frontal bone, the skull acceleration and intracranial pressure on different skull zones are performed according to the study of Nahum et al. [4]. The validation of the intra-cerebral acceleration and intracranial pressure is achieved based on the work of Troseille et al. [12]. Moreover, the skull fracture has been validated using the Yogonandan test [13]. Tolerance limits were established for this model by reconstructing 68 real world head traumas that occurred in motor sport, motorcyclist, American football and pedestrian accidents [11]. The model allows predicting three lesional effects: Diffuse Axonal Injury (DAI), subdural hematoma and skull fracture using respectively, Von Mises stress of the brain, strain energy of the CSF and strain energy of the skull as criteria. Table 2 gives the different tolerance limits corresponding to a probability of 50% injury risk [11,14].
3.2. Numerical Simulation of FN303 Impacts
The FN303 is a 17.3 mm diameter projectile from FN Herstal (Fig. 7). It is composed of a plastic hollow structure filled with bismuth powder and glycol. The projectile is designed to break at impact. The projectile mass is 8.5 g, and the average muzzle velocity is 90 ms-1 [15]. The finite element model of the FN303 projectile is shown in Fig. (8) [7, 15, 16]. The properties of the different parts of the model are summarized in Table 3. The projectile model is validated according to the force measurement on the rigid wall [7, 15]. The front, bottom and disk parts are made on polystyrene. The glycol is modelled as water. All parts were modelled with HEXA-elements except for the bismuth and the water modelled with Smoothed Particle Hydrodynamic (SPH) particles. Different contact types implemented in LS-DYNA are defined between the projectile model parts. A TIED_ SURFACE_TO_SURFACE contact is defined between the front and the bottom. AUTOMATIQUE_NODE_TO_ SURFACE contact is defined between the whole solid parts and the bismuth and water, respectively. A principal stress failure criterion for the polystyrene parts equal to 200 MPa was used [16].
Two impact configurations are considered: the temporal and the frontal impact (Fig. 9). The contact between the projectile and the SUFEHM is defined as AUTOMATIC_ NODES_TO_SURFACE. frontal.
The objectives of these impact simulations are:
- Determine the ICP and the maximum impact head force values at different velocities and compare those predicted by the force wall approach. This comparison is essential because the force wall approach is based on ICP / head force relation.
- Compare the maximum forces calculated by the SUFEHM and those predicted by the force wall approach.
- Compare the injuries defined by the force wall approach and those predicted by the SUFEHM.
The impact force is calculated at the interface between the projectile and the SUFEHM. However, some difficulties arose for the ICP measurement. In the DGA study, the ICP was measured at the cisterna magna while in the SUFEHM this part was not implemented. The alternative is to consider the maximum of the pressure in the CSF.
4. RESULTS AND DISCUSSIONS
4.1. Force Wall Approach Results
The results of the maximum force measurements on the rigid wall setup are presented in Fig. (10) and Fig. (11) for the XM1006 and the FN303, respectively. For each projectile, the relation of the maximum force and impact velocity is interpolated by a power curve. About 20 shots for each configuration should be performed to ensure statistically significant results. For technical limitations, only five shots were performed with XM1006. However, more than 20 shots were performed with the FN303, which improve the statistical reliability of the results. Table 4 gives the parameters of equation (2) for the FN303 and the parameters of equation (3) for the XM1006. The dispersions in terms of standard deviation (σ) are also presented, using a non-linear least squares regression. The correlation coefficients of the XM1006 test and the FN303 test are 0.980 and 0.995, respectively.
Based on these results, the head force curve of the FN303 is established. Fig. (12) shows the relation between the impact velocity and the head force of the FN303. The head force values are lower than those measured with the rigid wall structure for the same velocities.
According to the threshold force values given in Table 1, three benchmark velocities can be calculated using the curve shown in Fig. (12). For the FN303, the minimal velocity to have a skull fracture is 97 ms-1, which is however higher than the FN303 muzzle velocity. The force wall approach predicts that the FN303 projectile cannot cause skull fracture. It can although still cause unconsciousness if the impact velocity is greater than 55 ms-1 and meningeal damage if the impact velocity is greater than 79 ms-1. These impact velocities can be linked to shot distances based on the FN303 projectile retardation [7,15].
It appears that the force wall approach is an easy method to assess the non-lethal head impacts. It is clear that there are technical advantages to apply the force wall approach to obtain quickly a reliable head impact assessment. However, two issues remain to be investigated. On the one hand the method is based on the hypothesis that at the same maximum forces on the rigid wall, the effects on the head are equivalent. The relevance of this hypothesis should be verified using different approaches. That will be discussed in the following section. On the other hand, the proposed threshold values given in Table 1 are not linked to a probability of occurrence of damage. This problem can be solved for the bone damage by using the probability curve of the skull fracture proposed by Raymond [2]. Fig. (13) shows this probability curve giving the occurrence of fracture in terms of the maximum force for temporal impacts [2]. It appears that the value of 7.5 kN given in Table 1 corresponds to a probability of 80 % to have a fracture on the temporal part, according to the probability curve of Raymond. The proposed value used in the force wall approach seems to be consistent with the study of Raymond.
4.2. Comparison with the Numerical Model and the Mechanical Surrogate
The numerical model (SUFEHM) developed at Strasbourg University and the mechanical surrogate (BLSH) from Biokinetics are used in order to compare with the force wall approach results. The BLSH used in the current study is the property of TNO (Toegepast Natuurwetenschappeljk Onderzoek, Holland). The range of velocities is comprised between 20 ms-1 and 90 ms-1. This allows comparing the results in the whole interval in which the projectile is used.
Fig. (14) shows the comparison between the curve linking the ICP and the maximum head force calculated for the temporal and the frontal impacts with the SUFEHM and the curve given in Fig. (3) concerning the DGA results. Boundaries based on the maximum dispersion of the ICP results shown in Fig. (2), are added. For the temporal impact, consistent results were achieved as all data points are located within the boundaries and the general trend is good. These results confirm that the ICP curve from the DGA refers to the temporal impacts, especially for the high velocities. The choice of the maximum pressure calculated in the CSF is also coherent with the DGA results. The same findings were observed for another projectile in a previous study [17]. This first observation confirms that the relation used by the DGA to link the ICP for the head force is reliable.
Fig. (15) summarizes the different results obtained for the head force. In general, the trend is the same for all methods. There is a good agreement between the results of the SUFEHM and the force wall approach for the temporal impact. The computed average error is 6.98 % for the temporal impacts and 12.47 % for the frontal impacts. A good agreement of the results is also noted for the BLSH tests with average errors corresponding to the temporal and frontal impacts are 10.62 % and 8.35 %, respectively.
The last issue of the comparison concerns the injury prediction. The SUFEHM is used to predict the injury that can be caused by the FN303 impact. The threshold values presented in Table 2 are used. For our application, the SUFEHM does not predict a SDH or a DAI. The force wall approach indicates that there is a meningeal damage. The force wall injury descriptions are nevertheless not precise enough to be directly compared to SUFEHM. The fracture prediction will however constitute an interesting comparison point between the two methods.
Fig. (16) shows the evolution of the strain energy with the impact velocity. The threshold value for a skull fracture is 865 mJ. Therefore, there is a 50% of probability of skull fracture for temporal impacts at 60 ms-1 and for frontal impacts at 70 ms-1. An example of the predicted fracture for temporal impacts is shown in Fig. (17). The impact velocity of 60 ms-1 for the temporal impact corresponds to an impact force of 2.95 kN. According to the probability curve of Raymond, at this value, the probability of a skull fracture is 5 % (Fig. 13). The injury predictions of the SUFEHM are not the same compared to the force wall approach or Raymond study predictions. The shape, the caliber and the behavior during the impact of the projectiles used in the Raymond study or in the force wall approach (XM1006) are different from the FN303 projectile. That can explain the differences in the injury prediction. These parameters are essential for the occurrence of injuries and are not taken into account in the force wall approach. This issue should be investigated in order to define critical maximum impact forces according to these parameters. Nevertheless, the contact forces predicted by the SUFEHM are coherent with the forces calculated with the force wall approach or measured with the BLSH.
CONCLUSION
In this paper, a comparison was proposed between an original approach (force wall) to assess non-lethal projectile head impacts, a numerical model (SUFEHM) and a biomechanical surrogate (BLSH) for temporal and frontal impacts. The force wall approach is presented and applied for the FN303 projectile. This approach proposes a simple method to predict the maximum force and the injury that can result from a non-lethal impact on the head, using maximum force measurements on a rigid structure. The FN303 results show that the force wall approach can predict the relation between the maximum force on the head and the impact velocity. The proposed thresholds for the force wall approach are used to define critical velocities that correspond to unconsciousness, meningeal damage and bone damage, respectively.
In order to verify the consistency of the results, a surrogate and a numerical model were used. The SUFEHM predicts on the one hand the same relation between the ICP and the maximum impact force on the head, which is the base of the force wall approach. On the other hand, the maximum impact forces calculated with the SUFEHM are close to those predicted by the force wall approach. The same results are retrieved using the BLSH. Therefore, the results are consistent between these three approaches.
Despite the current limitations to carry out the injury assessment of the non-lethal projectiles head impacts, including accessibility to cadaveric data, the present work is the first study in the literature comparing assessment methods of the injury risk for such impacts. According to the different results, the force wall approach seems to constitute an alternative way to easily predict the maximum impact force that results from a non-lethal projectile impact. The SUFEHM and the BLSH predict equivalent maximum impact forces for non-lethal projectile head impacts. The maximum impact force seems to be a good predictor to assess the injury risk of the non-lethal projectile head impacts. These measurements and acceptable injury risk can then define an employment doctrine for non-lethal weapon users. Nevertheless, further investigations should be carried out in order to refine the critical thresholds of the maximum impact forces, including other parameters: the calibers, the shape and the behavior during the impact of the projectiles.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflicts of interest.
ACKNOWLEDGEMENTS
None Declared.


