All published articles of this journal are available on ScienceDirect.
3D DWT-DCT and Logistic MAP Based Robust Watermarking for Medical Volume Data
Abstract
Applying digital watermarking technique for the security protection of medical information systems is a hotspot of research in recent years. In this paper, we present a robust watermarking algorithm for medical volume data using 3D DWT-DCT and Logistic Map. After applying Logistic Map to enhance the security of watermarking, the visual feature vector of medical volume data is obtained using 3D DWT-DCT. Combining the feature vector, the third party concept and Hash function, a zero-watermarking scheme can be achieved. The proposed algorithm can mitigate the illogicality between robustness and invisibility. The experiment results show that the proposed algorithm is robust to common and geometrical attacks.
1. INTRODUCTION
Along with the rapid development of computer science and multimedia technology, the digital society gradually formed. Especially in the medical field, large amount of medical information exists as digital multimedia, such as text, video, voice and so on. It is convenient and fast for hospitals to store and transmit the patient’s personal information through the Internet. However, when the medical information is stored and transmitted on the Internet, it is extremely crucial to protect the patient's privacy [1-3]. Traditional digital watermarking technology is used in the copyright protection of digital media. Utilizing watermark's properties of invisibility and robustness, patient information, doctor diagnosis and Electronic Patient Records can be used as watermarking hidden in the CT, MRI (Magnetic Resonance Imaging) and other medical images [4]. Medical image digital watermarking is often divided into three categories [5].
1) RONI (Region of non-interest)-based medical image watermarking. The watermarking information is embedded in the RONI of the medical images [6, 7]. However, the capacity of hidden information is limited, as most of the RONI area of the medical image is the black background.
2) Reversible watermarking. When using reversible watermarking, once the embedded content is read, the watermarking can be removed from the image allowing retrieval of the original image [8]. Unfortunately, most of the reversible watermarking is fragile.
3) Classical watermarking. In this method, watermarking is often embedded in the least significant bit (LSB) [9], or in the low or middle frequency coefficients in the frequency domain (DCT, DFT or DWT) [10]. However, it is necessary to control the amount of the embedded watermarking to avoid the doctors making the wrong diagnosis. In addition, the classical watermarking has low robustness especially against common and geometric attacks.
More and more medical volume data appear along with the development of medical technology. Medical volume data contain more information, which can help the doctors understand the patient’s pathological information accurately so it is important, to research the digital watermarking of medical volume data.
In this paper, we propose a robust watermarking algorithm for medical volume data using the Logistic Map. Applying 3D DWT-DCT to acquire the visual feature vector of medical volume data, Zero-watermarking [11, 12] can be realized. We can scramble the watermarking using Logistic Map, which can enhance the security of watermarking. Combined with the third part concept and Hash function, we can embed and extract the watermarking of high quality. Meanwhile, the watermarking algorithm has good robustness to common and geometric attacks, which can protect the personal information of patients well.
2. THE FUNDAMENTAL THEORY
2.1. Logistic Map
A chaotic system has a noise like behavior while it is exactly deterministic, so we can reproduce it if we have its parameters and initial values. These signals are extremely sensitive to the initial conditions. One of the most famous chaotic systems is the Logistic Map, which is a nonlinear return map given by:
Where, xk((0,1) is the system variable, 0≤μ≤4 is the growth parameter, and k is the number of iterations. The study of the chaotic dynamical system shows that Logistic Map works in a chaotic state when 3.569945≤μ≤4. In this paper, we set μ=4. The chaotic sequences are generated by different initial values, x0. The Branch image of the Logistic Chaotic is shown in Fig. (1).
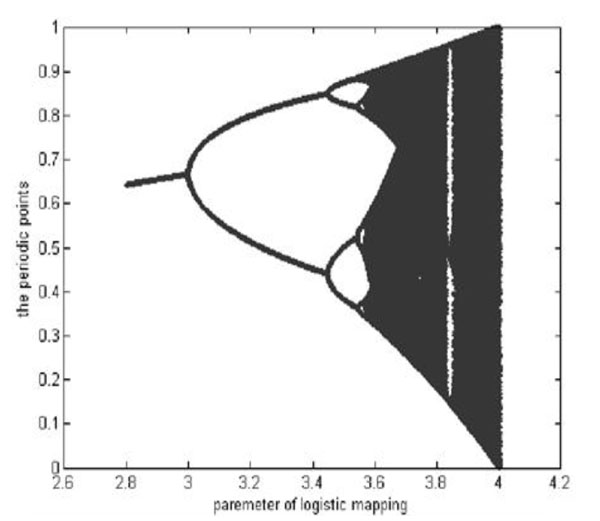
The branch image of the Logistic Mapping.
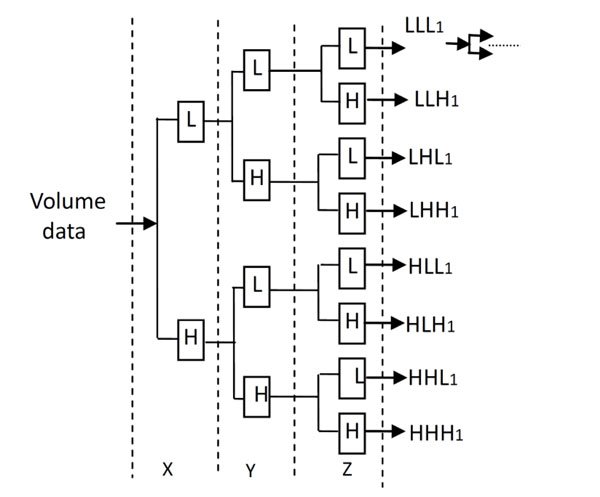
The Decomposition process of 3D Discrete Wavelet Transform.
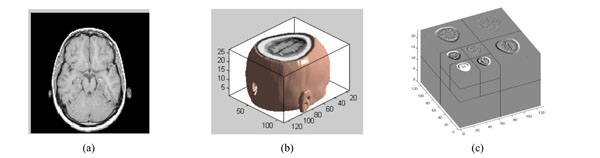
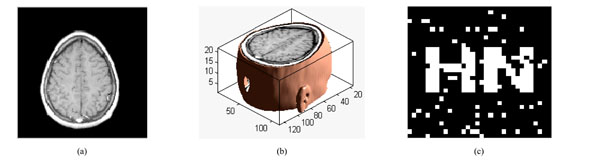
The three-dimensional discrete wavelet transform of medical volume data. (a) a slice of the medical volume data. (b) the corresponding three-dimensional reconstruction map. (c) the 3D-DWT of medical volume data (two layers).

Different attacks: (a) Original volume data; (b) Gaussian noise(3%); (c) JPEG compression(4%); (d) Median filter([3×3]) ;(e) Rotation(20°); (f) Scaling(0.5 times); (g) Translation(10%, down); (h) Cropping(8%, from z direction).
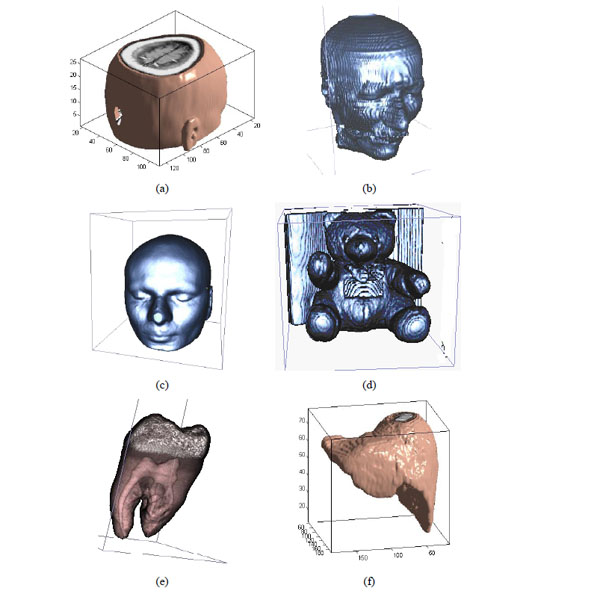
The different medical volume data.

Original watermarking and scrambled watermarking under Logistic Map (a)Original watermarking; (b) scrambled watermarking under Logistic Map.

watermarking under Logistic Map and restored watermarking (a) watermarking under Logistic Map (b)Restored watermarking.

Restoring watermarking; (a) The original watermarking; (b) The scrambled watermarking (c); The original medical volume data; (d) A slice of medical volume data.

Under Gaussian noise attack; (a) a slice of watermarked volume data under Gaussian noise (5%) ;(b) The watermarked volume data under Gaussian noise (5%) ;(c) the extracted watermarking.

Under JPEG attacks (2%); (a) a slice under JPEG attack; (b) the corresponding 3D volume data; (c) watermarking detector.
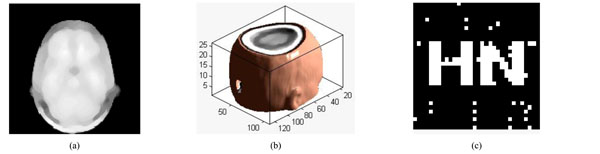
Under median filter attack. (a) The watermarked volume data under median filter (b) a slice of watermarked volume data under median filter (c) the extracted watermarking.
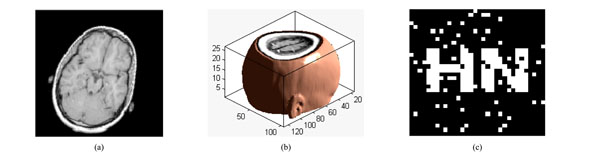
Under rotation attacks; (a) a slice of watermarked volume data rotated by 20° (b) The watermarked volume data rotated by 20° (c) the extracted watermarking
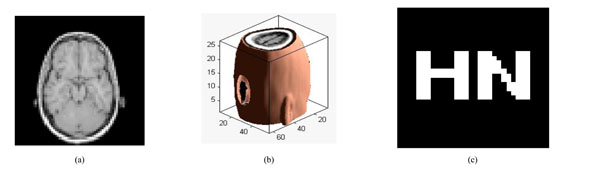
Under scaling attacks (factor 50%):; (a) a slice with scaling attack; (b) the corresponding 3D volume data; (c) watermarking detector.
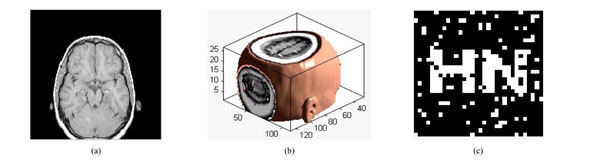
Under translation attacks (down8%): (a) a slice with translation attack; (b) the corresponding 3D volume data; (c) watermarking detector.
Under cropping attacks; (a) a slice of watermarked volume data cropped by 20%; (b) The watermarked volume data cropped by 20% (c) the extracted watermarking.
We can obtain the scrambled watermarking using the Logistic Map. The scrambled watermarking has the same size with the original one. In the same way, we can restore the original watermarking according to the same initial value based on the Logistic Map.
2.2. The 3D-Discrete Wavelet Transform and Example for Volume Data
The decomposition process of the 3D Discrete Wavelet Transform is shown in Fig. (2). L and H denote the low and high frequency component under low and high frequency filters respectively, which is similar to the 2D Discrete Wavelet Transform.
The medical volume data is decomposed in approximation coefficients (LLL1) which expresses low-frequency characteristic and the detail coefficients which express the high-frequency characteristic. The three-dimensional discrete wavelet transform of medical volume data is shown in Fig. (3). Fig. (3a) is a slice of the medical volume data, Fig. (3b) is the corresponding three-dimensional reconstruction map, Fig. (3c) shows the 3D-DWT of the medical volume data (two layers).
3. THE ALGORITHM
W={w(i,j)|w(i,j)=0,1;1≤i≤M1,1≤j≤M2} is used to represent the original watermarking. Meanwhile, one set of MRI medical volume data is selected as the original volume data, which is described as: F={f(i,j,k)|f(i,j,k)∈R;1≤i≤M, 1≤j≤N,1≤k≤P}. w(i,j) and f(i,j,k) represent the pixel gray value of the watermarking image and the voxel value of the original medical volume data. To facilitate the operation, we assume M1=M2, M=N.
3.1. Extracting the Feature Vector of Medical Volume Data Using 3D DWT-DCT
Applying 3D DWT-DCT, the feature vector of the medical volume data can be obtained. Feature vector of the medical volume data is a group of symbol sequence which represents the visual feature of the medical image. Firstly, 3D-DWT is applied to the original medical volume data to obtain the approximated sub-band LLL1. Then, DCT of the whole LLL1 is computed and the DWT-DCT coefficient is obtained. We choose 8 low-frequency 3D DWT-DCT coefficients (F(1,1,1), F(1,2,1),F(1,1,2),… F(1,2,4)) to compose the coefficient sequence of the volume data, the value of the low-frequency coefficients may change under some attacks. However, the signs of the coefficients remain unchanged, as shown in Table 1. The different attacked images are shown in Fig. (4a-4h). If the coefficient is positive or zero value, it is denoted as “1”; otherwise, it is denoted as “0”. Thus, we can obtain the sign sequence of low-frequency coefficients as shown in Table 1. We can see that the sign sequence remains unchanged after common and geometrical attacks.
Changes of the 3D DWT-DCT low-frequency coefficients with respect to different attacks.
| Image Processing | F(1,1,1) | F(1,2,1) | F(1,1,2) | F(1,2,2) | F(1,1,3) | F(1,2,3) | F(1,1,4) | F(1,2,4) | Sequence of Signs | NC |
|---|---|---|---|---|---|---|---|---|---|---|
| Original image | 14.25 | 0.52 | 1.73 | -0.29 | -2.27 | -0.13 | 0.98 | 0.11 | 11100011 | 1.0 |
| Gaussian noise(3%) | 22.12 | 0.41 | 1.89 | -0.18 | -2.22 | -0.09 | 1.23 | 0.08 | 11100011 | 1.0 |
| JPEG (4%) | 15.19 | 0.47 | 1.79 | -0.27 | -2.14 | -0.13 | 1.11 | 0.10 | 11100011 | 1.0 |
| Median filter [3x3] | 14.34 | 0.53 | 1.72 | -0.30 | -2.27 | -0.13 | 1.02 | 0.12 | 11100011 | 1.0 |
| Rotation 20° | 14.25 | 1.78 | 1.73 | -0.31 | -2.27 | -0.29 | 0.98 | 0.23 | 11100011 | 1.0 |
| MRI scaling (×2) | 28.55 | 1.05 | 3.47 | -0.58 | -4.56 | -0.26 | 1.96 | 0.22 | 11100011 | 1.0 |
| MRI scaling (×0.5) | 7.14 | 0.26 | 0.87 | -0.15 | -1.14 | -0.07 | 0.49 | 0.06 | 11100011 | 1.0 |
| Translation 10% | 13.74 | 0.51 | 1.56 | -0.29 | -2.00 | -0.12 | 1.02 | 0.10 | 11100011 | 1.0 |
| Crop (8% from Z) | 14.11 | 0.49 | 1.14 | -0.30 | -1.93 | -0.08 | 0.95 | 0.10 | 11100011 | 1.0 |
The NC values between feature vectors of different medical volume data using 3D DWT-DCT.( choose 8 bit)
| Volume Data | F (1,1,1) | F (1,2,1) | F (1,1,2) | F (1,2,2) | F (1,1,3) | F (1,2,3) | F (1,1,4) | F (1,2,4) | Sign Sequence | NC |
|---|---|---|---|---|---|---|---|---|---|---|
| Fig. 5 (a) | 14.24 | 0.52 | 1.70 | -0.29 | -2.21 | -0.13 | 0.85 | 0.09 | 11100011 | 1.00 |
| Fig. 5 (b) | 20.30 | -1.54 | -1.89 | 1.01 | -6.04 | 1.11 | 3.54 | -0.39 | 10010110 | -0.25 |
| Fig. 5 (c) | 32.54 | -25.57 | 14.71 | 32.24 | 30.31 | 15.78 | 1.35 | 14.10 | 10111111 | -0.42 |
| Fig. 5 (d) | 53.45 | -28.34 | 0.59 | -2.00 | -4.82 | 2.45 | 3.54 | -2.11 | 10100110 | 0.25 |
| Fig. 5 (e) | 54.9 | 0.21 | 0.475 | -0.19 | 1.88 | 0.18 | -0.79 | -0.33 | 11101100 | -0.06 |
| Fig. 5 (f) | 14.72 | 0.002 | -10.44 | 0.06 | -3.77 | 0.01 | 6.92 | -0.39 | 11010110 | -0.06 |
* the unit of transform coefficients is 1.0e+003.
The PSNR and NC under Gaussian noise attacks.
| Gaussian noise (%) | 3 | 5 | 10 | 15 | 20 | 25 |
|---|---|---|---|---|---|---|
| PSNR(dB) | 8.03 | 6.00 | 3.31 | 1.82 | 0.80 | 0.09 |
| NC | 0.95 | 0.95 | 0.89 | 0.88 | 0.86 | 0.80 |
The PSNR and NC under JPEG
| Compression quality (%) | 2 | 4 | 10 | 20 | 40 | 60 |
|---|---|---|---|---|---|---|
| PSNR(dB) | 16.57 | 17.82 | 20.20 | 23.10 | 25.06 | 26.61 |
| NC | 0.89 | 0.78 | 0.94 | 0.95 | 0.95 | 1.00 |
The PSNR and NC under Median Filter attacks
| Median Filter | [3x3] | [5x5] | [7x7] | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Repeat times | 1 | 10 | 20 | 1 | 10 | 20 | 1 | 10 | 20 |
| PSNR(dB) | 24.65 | 22.46 | 21.97 | 21.14 | 18.69 | 18.07 | 18.91 | 16.98 | 16.58 |
| NC | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 |
The PSNR and NC under rotation attacks
| Rotation | 5° | 10° | 15° | 20° | 25° | 30° | 35° | 40° |
|---|---|---|---|---|---|---|---|---|
| PSNR(dB) | 16.54 | 13.97 | 12.98 | 12.44 | 12.04 | 11.68 | 11.33 | 11.01 |
| NC | 0.87 | 0.87 | 0.87 | 0.87 | 0.83 | 0.83 | 0.83 | 0.71 |
The NC under scaling attacks
| Scaling factor | 0.2 | 0.5 | 0.8 | 1.0 | 1.2 | 2.0 |
|---|---|---|---|---|---|---|
| NC | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
The PSNR and NC under translation attack
| Down distance (%) | 2 | 4 | 6 | 8 | 10 | 12 |
|---|---|---|---|---|---|---|
| PSNR(dB) | 15.65 | 12.40 | 11.66 | 11.09 | 10.85 | 10.51 |
| NC | 1.00 | 1.00 | 0.94 | 0.82 | 0.61 | 0.61 |
The NC under cropping attacks
| Cropping(%) | 4 | 6 | 8 | 10 | 14 | 16 | 18 | 20 | 22 | 24 |
|---|---|---|---|---|---|---|---|---|---|---|
| NC | 1.00 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.88 | 0.88 | 0.82 | 0.82 |
Based on the above, we can draw a conclusion that the sign sequence of 3D DWT-DCT low-frequency coefficients can represent the main visual characteristics of the medical volume data and it is robust to common and geometrical attacks.
To prove that the sign sequence of 3D DWT-DCT for volume data is an important visual feature, we choose some different medical volume data which are shown in Fig. (5a-5f) and use 3D DWT-DCT transform. The coefficients and sign sequences of low frequency are different and the NC value between the different sign sequence is very small, and it is less than 0.5. It is shown in Table 2.
3.2. Scrambling the Watermarking
The steps of generating the scrambled watermarking are as follows:
Step1: Generate the chaotic sequence.
The chaotic sequence X(j) was generated by the initial value, x0, which is regarded as the private key. Each value of X(j) is between 0 and 1. The original watermarking cannot be recovered without the private key.
Step2: Obtain the scrambled watermarking.
First of all, the values of X(j) should be sorted in ascending order then the position of the values will change. According to the position change of the values we can scramble the position space of the watermarking image. In this way, the scrambled watermarking, BW(i,j), can be obtained. The original watermarking and scrambling watermarking are shown in Fig. (6).
3.3. Embedding Watermarking
Step3: Obtain the feature vector of the original volume data using 3D DWT-DCT.
Firstly, 3D-DWT is applied to decompose the original medical volume data F(i,j,k). Then we get the approximation coefficients FAL. Second, 3D-DCT is applied to the approximation coefficients to obtain the 3D DWT-DCT coefficient matrix DF(i,j,k). After arranging the 3D DWT-DCT coefficients from low to high frequency, the low-frequency sequence can be obtained, which is composed by the top L values. Finally, through the symbolic operation of the low-frequency sequence, the feature vector of the volume data, V(j)={v(j)|v(j)=0,1;1≤j≤L}, can be obtained. Here, the value of L can tune the robustness and capacity of the embedded watermarking. (In this paper, we set L=32 bits).
The process is as follows:
FAL(i,j,k)=DWT3(F(i,j,k))
DF(i,j,k)=DCT3(FAL(i,j,k))
V(j)=Sign(DF(i,j,k))
Step4: Obtain the key sequence.
The key sequence Key(i,j) can be computed through the feature vector V(j) and the scrambled watermarking BW(i,j) by HASH function:
Key(i,j)=V(j)⊕BW(i,j)
The key sequence Key(i,j) should be stored for extracting the watermarking later, and then we can get the ownership of the original volume data through registering the key sequence to the third part. The original volume data is of high quality without any effect, which is a zero- watermarking scheme.
3.4. Extracting Watermarking
Step5: Obtain the feature vector of tested volume data using 3D DWT-DCT.
The tested volume data is F’(i,j,k). This procedure of obtaining the feature vector V’(j) of the tested volume data is the same as Step 3 of watermarking embed. The process is as follows:
FA’L(i,j,k)=DWT3(F’(i,j,k))
DF’(i,j,k)=DCT3(FA’L(i,j,k))
V’(j)=Sign(DF’(i,j,k))
Step6: Extract the watermarking using the key sequence Key(i,j).
Combining the key sequence Key(i,j) and the feature vector of the tested volume data V’(j), the watermarking can be extracted as follows:
BW’(i,j)=Key(i,j)⊕V’(j)
The extracted watermarking is scrambled. No useful information is obtained after that, and therefore, we must restore it so as to get the accurate information.
3.5. Restoring Watermarking
The chaotic sequence X(j) can be obtained by the same initial value using Logistic Map. By sorting the values of X(j) in ascending order, we can restore the scrambled watermarking according to the position change of X(j). Finally, we can get the restored watermarking W’(i,j). The scrambled watermarking and the restored watermarking are shown in Fig. (7).
4. EXPERIMENTS
To verify the effectiveness of our proposed algorithm, we carried out the simulation in Matlab2010a platform. Choosing a significant binary image as the original watermarking, which is described as: W={w(i,j)|w(i,j)=0,1; 1≤i≤32,1≤j≤32}, shown in Fig. (8a); Fig. (8b) is the scrambled watermarking using Logistic Map. It clearly shows that great changes have occured to the watermarking, which improves the security of watermarking. At the same time, we select one set of MRI medical volume data as the original medical volume data, which is described as: F={f(i,j,k)|f(i,j,k)∈R; 1≤i≤128,1≤j≤128,1≤k≤27}, shown in Fig. (8c). Fig. (8d) is a slice of the original medical volume data. In the simulation, we set x0=0.2, u=4.
After extracting the watermarking W’(i,j), we can use the Normalized Cross-correlation(NC) to measure the quantitative similarity between the extracted and embedded watermarking, The higher the NC value, the more similarity there is between the embedded and extracted original watermarking. W(i,j) represents the original watermarking and W’(i,j) represents the extracted original watermarking.
The followings are several types of attacks to test the robustness of the algorithm.
4.1. Common Attacks
4.1.1. Adding Gaussian Noise
Gaussian noise is added by the imnoise() function with different noise intensity in the watermarked volume data. Fig. (9a) is a slice of medical volume data under Gaussian noise (5%). The medical volume data under Gaussian noise (5%) is very blurry with PSNR=6.00dB, shown in Fig. (9b). However, the watermarking can be extracted with NC=0.95, the extracted watermarking is clear, shown in Fig. (9c).
From Table 3, we can see that the watermarking can be extracted exactly, even when the noise intensity is up to 25%. So the proposed algorithm has good robustness to Gaussian noise attacks.
4.1.2. JPEG Attacks
The slice under JPEG attacks (2%) is shown in Fig. 10(a) and the corresponding 3D image of volume data with PSNR of 16.57dB is shown in Fig. (10b). The slice and volume data becomes blur. Fig. (10c) show the watermarking can still be detected, NC=0.89. Table 4 gives the PSNR and NC when the volume data is under JPEG attacks by different parameters. If the compression quality is down to 2%, then the watermarking can still be detected, NC=0.89, It proves that the algorithm is robust against JPEG attacks.
4.1.3. Median Filter Processing
We can make the filter impact on the watermarked volume data with different size of median filter and the repeat number of filtering. A slice of volume data is shown in Fig. (11a); The volume data under median filter attack [5×5] is shown in Fig. (11b), it can easily to be seen that the contour of ear is not too clear, PSNR=18.69dB. The watermarking can be extracted with NC=0.95 shown in Fig. (11c). The extracted watermarking is almost the same to the original one. From Table 5, we can see that the watermarking can still be extracted even when the parameter of Median Filter is [7×7], repeat times are 10. Thus, we can conclude that the proposed algorithm is robust to Median Filter attacks.
4.2. Geometrical Attacks
4.2.1. Rotation Attacks
The slice rotated by 20° is shown in Fig. (12a), and the corresponding 3D image of volume data is shown in Fig. 12(b). The watermarking can be extracted with NC=0.87 and PSNR=12.44dB, shown in Fig. (12c). The watermarking can still be extracted even when the watermarked volume data rotated clockwise by 40°, shown in Table 6. Thus, the proposed algorithm has strong robustness to rotation attacks.
4.2.2. Scaling Attacks
Fig. (13a) is a slice of the watermarked volume data under scaling attack. Fig. (13b) shows that the Volume data shrunk with a scale factor of 0.5. We can still extract the watermarking accurately with NC=1.0, shown in Fig. (13c). The watermarking can still be extracted even when the watermarked volume data shrunk with a scale factor of 0.2, shown in Table 7. Thus, the proposed algorithm has strong robustness to scaling attacks.
4.2.3. Translation Attacks
The slice under translation down by 8% is shown in Fig. (14a) and the corresponding 3D image of volume data is shown in Fig. (14b). The PSNR of the translated volume data is 11.09dB. Fig. (14c) show that the watermarking can still be detected, NC=0.82. Table 8 gives the PSNR and NC when the volume data has been translated by different distance. Hence, we can conclude that the algorithm is robust against translation attacks.
4.2.4. Cropping Attacks
Fig. (15a) is a slice of the watermarked volume data under cropping attack. The watermarked volume data has been cropped 20% from Z direction, shown in Fig. (15b); we can see clearly that the main information loss is at the top of volume data. We can still extract the watermarking accurately with NC=0.88, shown in Fig. (15c). Through the experimental data of Table 9, we can find that the watermarking can still be extracted under cropping attack 24%. Therefore, the proposed algorithm is robust to cropping attacks.
5. CONCLUSION
In this paper, we proposed a robust watermarking algorithm for medical volume data. The watermarking is scrambled by Logistic Map to improve its security. Applying 3D DWT-DCT, the visual feature vector of medical volume data is obtained. Combining the feature vector, the third part concept and Hash function, a zero-watermarking scheme can be achieved. Experimental results show that the watermarking can still be extracted accurately without the original medical volume data, which achieves the blind extracting and protects the medical volume data adequately. Moreover, the proposed algorithm has strong robustness to common and geometrical attacks.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflicts of interest.
ACKNOWLEDGEMENT
This work is supported by the National Natural Science Foundation of China (No: 61263033) and the NSF of Hainan Province of China (No: 60894).


