RESEARCH ARTICLE
Complete Unsteady One-Dimensional Model of the Net Aortic Pressure Drop
Francesca M. Susin1, *
Article Information
Identifiers and Pagination:
Year: 2019Volume: 13
First Page: 83
Last Page: 93
Publisher ID: TOBEJ-13-83
DOI: 10.2174/1874120701913010083
Article History:
Received Date: 14/02/2019Revision Received Date: 13/05/2019
Acceptance Date: 22/05/2019
Electronic publication date: 30/06/2019
Collection year: 2019

open-access license: This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International Public License (CC-BY 4.0), a copy of which is available at: https://creativecommons.org/licenses/by/4.0/legalcode. This license permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Background:
A large amount of engineering and medical research has been devoted to the assessment of aortic valve stenosis severity in the past decades. The net transvalvular pressure drop has been recognized as one of the parameters that better reflect stenosis effects on left ventricle overload, and its adoption in clinical assessment of stenosis has been proposed. Flow unsteadiness has been shown to have a non-negligible impact on the net drop; however, a simple formulation for net drop calculation that includes not only flow pulsatility but also the effects of valve dynamics is still lacking.
Objective:
The present contribution is hence aimed at developing a complete unsteady one-dimensional model of the net aortic transvalvular pressure drop that just requires non-invasive data to be implemented.
Methods:
Transvalvular flow is described as a jet of incompressible viscous fluid through a circular orifice placed in a concentric rigid circular tube. The classical one-dimensional mass and total head conservation equations are applied. The effective orifice area and transvalvular flow rate are assumed to vary with time throughout the ejection period.
Results:
The model is found to capture pressure drop oscillations occurring when the valve opens/closes and/or leaflets flutter, thanks to the inclusion of valve dynamics effects. The model is also proposed as a numerical tool for the calculation of the instantaneous effective orifice area once net pressure drop and flow rate are known.
Conclusion:
The model may contribute to the improvement of non-invasive aortic stenosis assessment.
1. INTRODUCTION
Clinical non-invasive assessment of heart valves hemodynamics and in-vitro assessment of prosthetic valves performance are fundamental issues widely investigated in the literature in the past decades. The unanimous objective is the development of reliable tools that can help clinicians in the diagnosis and therapy of valvular diseases [1-8], and support the development of safe and effective heart valve substitutes [9-13].
Native aortic valve stenosis (AS) is the most common valvular disease in the western countries, and its incidence is destined to increase due to the aging population. It is a pathologic state characterized by a valvular orifice area smaller than the healthy one. Blood ejected from the left ventricle through the narrowed orifice experiences a sort of obstruction, and is affected by pressure loss due to turbulence just downstream of the valve. The left ventricle is hence forced to work against an increased afterload. AS can be either congenital or acquired. In the first case, bicuspid aortic valve is the most frequent valvular anomaly that leads to stenosis, in infancy or later in time [14]. In the second case, the usual degenerative process is a progressive calcification of valvular leaflets [15]. Whatever the etiology, management of stenotic patients is of great importance since progression of the disease, whether untreated, is fatal [5]. Accurate assessment of stenotic lesion gravity is then crucial for patient treatment and for the selection of the appropriate timing for surgical or transcatheter valve replacement [3]. Graduation of the pathology by comparison of estimated values to reference cutoff given in international guidelines [16] usually proves effective for the majority of patients. Nevertheless, the debate around the improvement of assessment of aortic stenosis is far from being concluded yet, as demonstrated by recent comprehensive reviews on the topic [3, 5, 17]. This is mainly due to the complexity of both the pathology, often coupled to commorbidities, and valvular solid and flow mechanics. We refer to the above reviews for a detailed panorama of possible inconsistencies between guidelines and improved diagnostics, and a description of related parameters. Here, we are interested in recalling that one of the hemodynamic indexes currently adopted to grade the severity of the stenotic lesion is the maximum transvalvular pressure drop Δpmax [5, 16, 18]. Indeed, it has been demonstrated that the pressure difference that better reflects the increased ventricular workload in aortic stenosis is the net transvalvular drop Δpnet [19, 20], which has been suggested as a possible better index of stenosis severity [4, 21]. Moreover, it has been widely recognized that inconsistencies in the graduation of stenosis severity when obtained from Doppler and catheterization, respectively, can be mainly ascribed to the fact that Doppler measurements estimate Δpmax while catheterization usually measures Δpnet [3].
Some theoretical models have been proposed in the literature to predict the instantaneous pressure difference across both native and prosthetic aortic valves [19, 22-25]. In particular, Garcia and co-authors have derived a simple and effective analytical expression for Δpnet that can be implemented with Doppler echocardiographic measurements [19]. Their theoretical approach accounted for transvalvular pulsatile flow rate and assumed constant effective orifice area during the ejection period. The extensive series of experiments performed with either rigid orifice plates or bioprosthetic valves (i.e. flexible orifices) proved the capability of the model to reliably reproduce the measured net pressure drop. However, some difference between predicted and measured Δpnet can be appreciated in the early systole of bioprosthetic in-vitro tests due to the presence of pressure drop oscillations and related peak, suggesting that valve dynamics may affect the behaviour of the instantaneous net pressure drop. As far as aortic valve dynamics is concerned, it is widely recognized that normal native and well-functioning prosthetic valves usually open and close very rapidly, and fairly stay at maximal opening during most of the systolic period [26-32]. On the contrary, stenotic valves not only exhibit a smaller geometric and effective orifice area at maximal opening, but also open and close more slowly [26-33]. In that case, the assumption of constant area during the systole to estimate the transvalvular net pressure difference might deserve some further investigation.
Following the above observations, the present study is aimed at extending the approach proposed by Garcia and colleagues [19] to develop a simple model of transvalvular flow that includes inertia terms associated not only with flow pulsatility but also with valve area unsteadiness. The theoretical analysis is detailed in Section 2, together with the description of numerical tests performed for model validation. Section 3 describes the results, which are then discussed and commented on in Section 4. Finally, Section 5 is devoted to some conclusion.
2. MATERIALS AND METHODS
2.1. Background
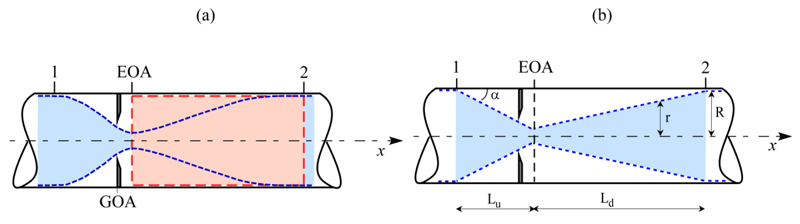
The instantaneous flow pattern across a stenotic aortic valve during systolic ejection is usually modelled as a jet through a circular orifice placed in a concentric circular tube that mimics the anatomical district between the left ventricle outflow tract and the ascending aorta [18, 19, 34-36]. The configuration of the jet through the orifice is sketched in Fig. (1), with the adopted notations. In order to pass the stenotic obstruction, the approaching flow contracts from some distance upstream the orifice (location 1, Fig. 1) up to the vena contracta, the so called Effective Orifice Area (EOA), i.e. the smaller area of the transvalvular jet. It then expands and reattaches to the wall at some distance downstream in the aortic tube (location 2). Turbulent recirculation with a complicated eddying behaviour occurs adjacent to the jet in the expansion region and produces energy losses [37], implying a pressure drop between location 1 and location 2.
Energy dissipation is not the only mechanism that drives pressure difference between the left ventricle and the ascending aorta, but both convective and temporal acceleration of the flow also act [19, 23]. The former is related to the possible difference in the cross-sectional area of the left ventricular outflow tract and the ascending aorta, respectively. The latter is due to the unsteadiness of the flow. In the blood flow through aortic valve, not only the flow rate but also the geometrical orifice area varies in time [26, 27, 30]. As a consequence, the configuration of the whole jet through the orifice (length and cross-sectional area) varies in time as well (flow configuration at different times is depicted in Fig. 1b). In particular, EOA dynamics typically exhibits opening, fairly constant, and closing phases with rate of change that is basically driven by stenosis level [29, 38]. In addition, a wavy behaviour can be usually recognized in proximity of the maximum area, EOAmax due to leaflets fluttering [39, 40]. Notice that this behaviour is observed also for the prosthetic valves [41-44].
The scenario here described is the focus of the model developed in the following section.
2.2. Analytical Model of Δpnet
Some assumptions are required to develop the mathematical formulation of the pressure drop experienced by blood flow between locations 1 and 2 in Fig. (1a). Firstly, blood is considered Newtonian and incompressible, and non-deformable walls are assumed for the tube, i.e., the area A of the tube is constant not only along its axis x but also in time t. As a result, from mass conservation, the instantaneous flow rate Q(t) turns out to be the same at each tube section. Secondly, the area of the orifice is assumed to vary in time and, as a consequence, the whole transvalvular jet dynamics is accounted for. This latter assumption implies that, in particular, the effective orifice area and the length of the jet are time-dependent, i.e. EOA(t) and L(t) have to be considered.
By neglecting the weight of the fluid in the tube [19], the total head of the flow at any section, H is
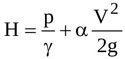 |
(1) |
where g is gravity, γ is the specific weight of the fluid, p is the pressure, V is the average flow velocity (i.e. the ratio of the flow rate to the jet cross-sectional area), and α is a correction factor which accounts for non uniform velocity distribution across a given cross-section [45]. Notice that V, p and H are all time-dependent.
The total head at any time varies with the distance along the flow direction, x according to the following equation [37]
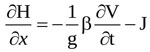 |
(2) |
where J is the head loss per unit length of flow, and β is another correction factor accounting for non-uniform velocity distribution. Here, almost uniform velocity profiles are assumed at any section along the jet [19, 35], so that 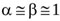 .
.
Equation (1) shows that the instantaneous pressure difference Δpnet=(p1-p2)/γ, i.e. the net pressure drop across the orifice, is equal to the instantaneous total head difference (H1-H2) since sections 1 and 2 have the same cross-sectional area and, hence, the same average velocity. Hence, from integration of Equation (2) between locations 1 and 2, Δpnet is obtained
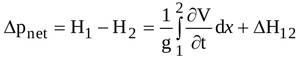 |
(3) |
where 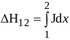 is the head loss due to both viscous shear along the wall and boundary layer separation. For orifice flow, the latter source of loss is larger than the former one [45], and is therefore the only contribution taken into account here. Moreover, turbulent recirculation mainly affects the flow from EOA location to location 2, so that Δh12 = ΔhEOA2 is assumed [46].
is the head loss due to both viscous shear along the wall and boundary layer separation. For orifice flow, the latter source of loss is larger than the former one [45], and is therefore the only contribution taken into account here. Moreover, turbulent recirculation mainly affects the flow from EOA location to location 2, so that Δh12 = ΔhEOA2 is assumed [46].
The head loss ΔhEOA2 can be obtained by integrating equation (2) from EOA to location 2, and is expressed as
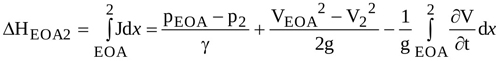 |
(4) |
In order to express the pressure difference =(pEOA-p2)/γ in terms of average velocities, the momentum equation along x is applied to the control volume Ω shown in Fig. (2a)
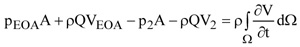 |
(5) |
Recalling that dΩ=Adx, and Q=AV2, Equation (5) gives
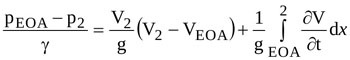 |
(6) |
Equations (3), (4), and (6) then give
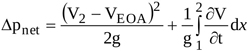 |
(7) |
According to mass conservation one has Q=EOA.VEOA=AV2=AxV, and Equation (7) is hence rewritten as
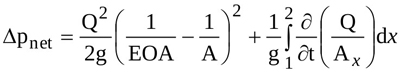 |
(8) |
Moreover, recalling that Q=Q(t) and Ax=Ax (x,t), the local inertia term on the right side of Equation (8) can be splitted in two terms, so that Δpnet is expressed as
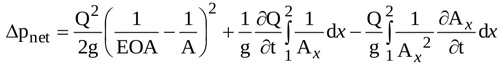 |
(9) |
the three terms on the right hand side being the head loss term (ΔLoss), the inertia term depending on flow pulsatility (flow inertia, ΔfI), and the inertia term related to the time variability of transvalvular jet geometry (jet inertia, ΔjI), respectively. Notice that the latter is the novel contribution proposed by the present model.
Both ΔfI and ΔjI require the instantaneous geometry of the jet (i.e. Ax(x,t)) to be evaluated. In order to obtain an analytical formulation for them, the contracting and the expanding jet are assumed conical (Fig. 2b). Equation (10) can thus be rearranged (see Appendix for details)
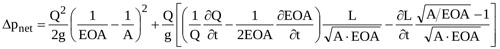 |
(10) |
where L is the instantaneous total length of the jet.
Time behaviour of the total length of the jet, L is required to calculate the instantaneous net pressure difference as given by Equation (10). For conical jet configuration the following relation holds (see Appendix)
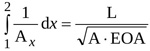 |
(11) |
Moreover, according to Garcia and colleagues [19] it turns out that
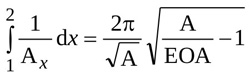 |
(12) |
Hence, from Equations (11) and (12), the length of the jet can be expressed as
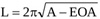 |
(13) |
so that, with Equation (13), Equation (10) finally reads
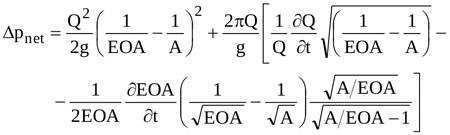 |
(14) |
Equation (14) can hence be adopted to predict the waveform of Δpnet for assigned values of A and temporal distribution of the ejected Q(t) once EOA(t) is known.
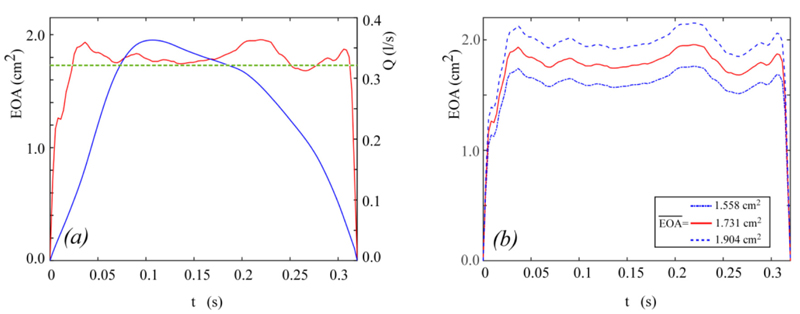 |
Fig. (3). Panel a: the in-vitro flow rate (blue line, taken from Fig. 4 of [19]) and effective orifice area (red line, taken from [29]) waveforms adopted for the complete unsteady Δpnet model validation. The green dotted line corresponds to the mean effective orifice area according to [19]. Panel (b): EOA(t) waveforms adopted for the sensitivity analysis as 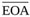 varies. varies. |
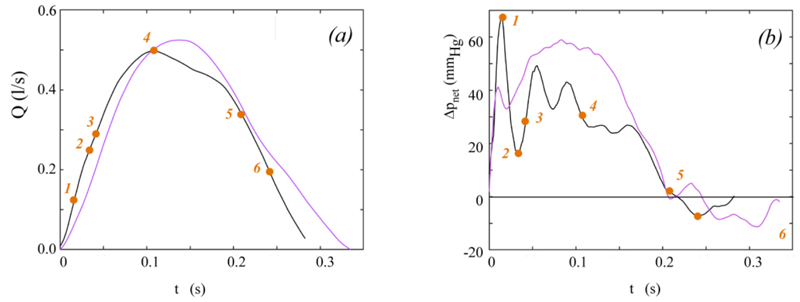 |
Fig. (4). in-vitro flow rate (panel a) and net pressure drop (panel b) used as input for Equation (15) solution. Black lines show data taken from [23], purple lines show data taken from [19]. Orange dots mark significant time points (see also Fig. (6). |
2.3. The Model of ΔPnet as a Numerical Tool for EOA(t) Calculation
Equation (14) can be rearranged to obtain the rate of change of the effective orifice area
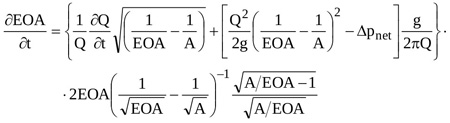 |
(15) |
Equation (15) is a nonlinear partial differential equation of the first order in EOA that can be solved numerically for given temporal distributions of Δpnet(t) and Q(t). Here a 4th order Runge-Kutta scheme is adopted, for prescribed initial condition EOA(t0)=EOA0.
2.4. Numerical Tests
Data from published in-vitro tests [19] are here used to validate Equation (14). In particular, the waveforms of p1, p2, and Q drawn in Fig. (4) of [19] are digitized in the ejection period Tej to obtain the numerical values of these quantities. The instantaneous derivative ∂Q/∂t required in Equation (14) is approximated by central differences. In addition, an aortic area A=800 mm2 and a fluid density ρ=1008 kg/m3 are assumed, as in the experimental test [19]. Unfortunately, the temporal distribution of the effective orifice area is not given in [19]. A realistic behaviour is hence here reconstructed as follows. The non-dimensional effective orifice area EOAnd(t)=EOA(t)/ EOAmax given in [29] for aortic healthy valve is assumed, with open valve duration Top equal to Te. Moreover, the maximum area EOAmax is estimated as
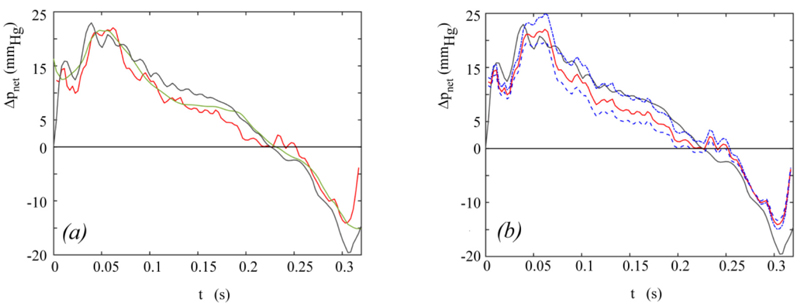 |
Fig. (5). Net pressure drop model validation and sensitivity analysis results. Panel a: in-vitro (grey line) and predicted net pressure drop (red line: present Δpnet model; green line: model given in [19].  = 1.731 cm2 for both models). Panel b: grey and red lines as in panel a; blue lines: Δpnet as predicted by the present model for = 1.731 cm2 for both models). Panel b: grey and red lines as in panel a; blue lines: Δpnet as predicted by the present model for  = 1.558 cm2 (upper line) and = 1.558 cm2 (upper line) and 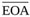 = 1.904 cm2 (lower line), respectively in-vitro data are taken from [19]. = 1.904 cm2 (lower line), respectively in-vitro data are taken from [19]. |
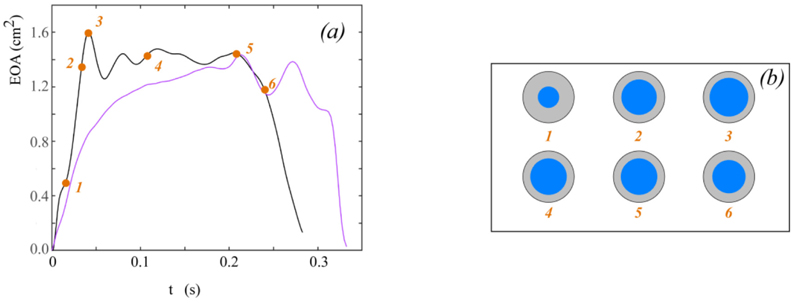 |
Fig. (6). Instantaneous effective orifice area calculated by solving Equation (15) (colours as in Fig. 4). Panel (d): schematic representation of calculated EOA(t) at significant time points for data taken from [23]. Orange dots mark significant time points (see also Fig. (4). |
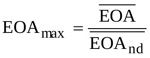 |
(16) |
where the overbar denotes the mean over the ejection period. Finally, the mean area 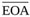 is calculated by adopting the formula reported by Garcia and colleagues [19]
is calculated by adopting the formula reported by Garcia and colleagues [19]
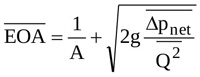 |
(17) |
For the in-vitro conditions taken from [19] and here considered, 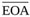 = 1.731 cm2. The behaviour of Q(t) and EOA(t) obtained in the above way and implemented in Equation (14) is shown in Fig. (3a).
= 1.731 cm2. The behaviour of Q(t) and EOA(t) obtained in the above way and implemented in Equation (14) is shown in Fig. (3a).
It is worthwhile underlining that Equation (17) was obtained in [19] under the hypothesis that the valve dynamics keeps constant in time. As a consequence, the mean effective orifice here calculated is somehow different from the actual one. For that reason, the sensitiveness of Δpnet to the value assigned to 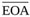 is here investigated by implementing Equation (14) for
is here investigated by implementing Equation (14) for 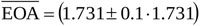 cm2, while maintaining EOAnd(t) and Q(t) unchanged. Notice that as
cm2, while maintaining EOAnd(t) and Q(t) unchanged. Notice that as 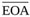 varies the rate of change ∂EOA/∂t proportionally varies (i.e. larger/smaller
varies the rate of change ∂EOA/∂t proportionally varies (i.e. larger/smaller 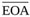 implies faster/slower EOA variation in time). Fig. (3b) shows the different waveforms of EOA(t) here adopted for the sensitivity analysis.
implies faster/slower EOA variation in time). Fig. (3b) shows the different waveforms of EOA(t) here adopted for the sensitivity analysis.
Further tests are here performed to explore the capability of the model of Δpnet to serve as a numerical tool for EOA(t) calculation. In this series of tests, Q(t) and Δpnet(t) waveforms measured in two different literature in-vitro experiments are used as input of the numerical scheme adopted to solve Equation (15). The considered data are shown in Figs. (4a) and (4b). They have been measured for a bileaflet mechanichal valve (Saint Jude Hp 19 mm, [23]), and for a biological valve (Mosaic 21 mm, [19]), respectively. Notice that since the flow rate corresponding to the Mosaic 21 mm valve experiment has not been reported in [19], it is here calculated according to the following approach. First, the analytical model of the net pressure gradient proposed in [19] is rewritten in the form:
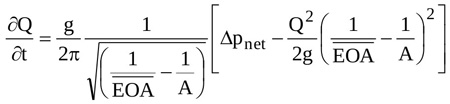 |
(18) |
Second, the instantaneous net pressure drop for the Mosaic 21 mm valve predicted by Garcia and co-authors is digitized from Fig. (6) of [19]; notice that the corresponding 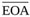 is also reported in the that figure, and the ventricular-aortic area A is reported in the text. Finally, Equation (18) is solved for the aforesaid values of Δpnet,
is also reported in the that figure, and the ventricular-aortic area A is reported in the text. Finally, Equation (18) is solved for the aforesaid values of Δpnet, 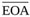 and A, so that the instantaneous experimental Q(t) is obtained. In both the present numerical tests, integration of Equation (15) starts from an instant t0 immediately after the beginning of ejection (i.e., immediately after the valve starts to open) so that the initial value EOA(t0)=EOA0 is small but not null.
and A, so that the instantaneous experimental Q(t) is obtained. In both the present numerical tests, integration of Equation (15) starts from an instant t0 immediately after the beginning of ejection (i.e., immediately after the valve starts to open) so that the initial value EOA(t0)=EOA0 is small but not null.
3. RESULTS
The instantaneous net pressure drop predicted by the present model for the hemodynamic conditions depicted in Fig. (3a) is shown in Fig. (5a), together with the Δpnet waveform measured in in-vitro tests [19]. The instantaneous net pressure drop predicted by the model given in [19] for an effective orifice area constant in time and equal to 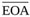 = 1.731 cm2 is also shown for comparison.
= 1.731 cm2 is also shown for comparison.
The results of the sensitivity analysis of Equation (14) performed by varying the mean effective orifice area 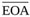 are reported in Fig. (5b).
are reported in Fig. (5b).
Fig. (6a) shows the instantaneous effective orifice area in time as calculated from Equation (15) for the experiments reported in the two studies [23] and [19], respectively. For the experiment reported by Fiore et al. [23], the schematic representation of the effective orifice area cross-section at significant time points is also given for a comprehensive view of the phenomenon (Fig. 6b).
4. DISCUSSION
The complete unsteady Δpnet model here proposed can be regarded as an upgrade of that developed earlier [19]. Basically, the hypotheses adopted to describe the flow across an aortic valve are the same but, as novel contribution of the present work, the effects of valve dynamics are accounted for. Moreover, the transvalvular flow pattern is here modelled as a conical jet, which allows the analytical integration of the inertia term and leads to Equation (10), with Δpnet(t) expressed as a function of Q(t), EOA(t) and L(t). In particular, it is found that: i) transvalvular jet inertia contributes to Δpnet through the rate of change of both the effective orifice area, EOA and the length of the jet, L; ii) time-variability of EOA affects not only the novel jet inertia term ΔjI but also the flow inertia term ΔfI and the head loss term ΔLoss, since they both depend on EOA(t); iii) for rigid orifices (i.e.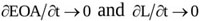 ) Equation (10) reduces to the model developed by Garcia and colleagues [19] following a semi-empirical approach, thus corroborating the present choice of a conical shape for the converging/ diverging transvalvular jet.
) Equation (10) reduces to the model developed by Garcia and colleagues [19] following a semi-empirical approach, thus corroborating the present choice of a conical shape for the converging/ diverging transvalvular jet.
A simpler formulation of the model is also given (Equation (14)), which can be easily implemented once purely kinematic and geometrical quantities (Q(t), EOA(t), and A) are known. Notice that the required data can be obtained by routine Doppler echocardiography for both the in-vitro and in-vivo case, i.e. the model allows non-invasive estimation of Δpnet. Equation (14) is validated by comparing its prediction to published experimental data and to the results provided by the model given in [19] (Fig. 5a). The ability of the present model to capture Δpnet oscillations occurring at early/late ejection as the valve rapidly opens/closes clearly appears from the comparison. Moreover, the wavy Δpnet behaviour due to valve leaflets fluttering in the open valve phase is well reproduced. Hence, both these features actually result to be the footprints of the valvular dynamics, since they are reproduced only when valve dynamics effects are accounted for. It is worthwhile now recalling that the behaviour of EOA(t) adopted in Equation (14) validation is not the real one but a realistic reconstruction, built from in-vivo measurements of healthy aortic valve dynamics. The mean effective orifice area, which is also required to reconstruct EOA(t), is estimated from the theory reported in [19], i.e. under the hypothesis of valve dynamics constant in time. The results of the sensitivity analysis performed on Equation (14) for values of 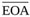 around such an estimate show that the correspondence between the predicted and the in-vitro Δpnet can even improve if an appropriate
around such an estimate show that the correspondence between the predicted and the in-vitro Δpnet can even improve if an appropriate 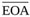 is adopted (Fig. 5b). That is, a very good match between the calculated and the experimental net pressure drop is likely to result when the real rather than the reconstructed EOA(t) is available. However, it is worthwhile pointing out that the difference between the net pressure drop predicted by Equation (14) for
is adopted (Fig. 5b). That is, a very good match between the calculated and the experimental net pressure drop is likely to result when the real rather than the reconstructed EOA(t) is available. However, it is worthwhile pointing out that the difference between the net pressure drop predicted by Equation (14) for 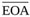 = 1.731 cm2 and the experimental one shown in Fig. (5a) results to be less than 5 mmHg (i.e. in the range of clinical accuracy) in the entire ejection period, apart from the late systole, when valve closure occurs and the difference reaches a maximum of about 10 mmhg. This latter result, which is however limited to a narrow time span, suggests that the predicted Δpnet is likely quite sensitive to the actual EOA(t) in the final valve closing phase. All the above results strengthen the idea that aortic valve dynamics plays a non-negligible role on the time evolution of net pressure drop across the valve. Despite the overall complexity of the flow field, such a contribution seems to be accurately predicted by the simple one-dimensional approach here proposed. Interestingly, the analytical expression of the jet inertia term ΔjI in Equation (14) shows that it has a sign opposite to that of the flow inertia term ΔfI, so that a reduction of Δpnet is favoured while the flow rate increases.
= 1.731 cm2 and the experimental one shown in Fig. (5a) results to be less than 5 mmHg (i.e. in the range of clinical accuracy) in the entire ejection period, apart from the late systole, when valve closure occurs and the difference reaches a maximum of about 10 mmhg. This latter result, which is however limited to a narrow time span, suggests that the predicted Δpnet is likely quite sensitive to the actual EOA(t) in the final valve closing phase. All the above results strengthen the idea that aortic valve dynamics plays a non-negligible role on the time evolution of net pressure drop across the valve. Despite the overall complexity of the flow field, such a contribution seems to be accurately predicted by the simple one-dimensional approach here proposed. Interestingly, the analytical expression of the jet inertia term ΔjI in Equation (14) shows that it has a sign opposite to that of the flow inertia term ΔfI, so that a reduction of Δpnet is favoured while the flow rate increases.
The present theoretical framework on transaortic hemodynamics also provides a partial differential equation for the effective orifice area rate of change. This tool can be adopted to calculate EOA(t) once the flow rate and net pressure drop are known. Numerical solution of this equation for two literature cases (Fig. 5a) indicates that all the fundamental phases and features that typically mark aortic valve/jet dynamics (opening, maximum opening and concurrent fluttering, closing) are effectively reproduced. Indeed, EOA(t) exhibits a behaviour remarkably similar to what obtained in in-vivo, in-vitro and (sophisticated) in-silico investigations for either the geometrical, the projected, and the effective orifice area [25, 38, 40, 47, 48]. Notice that although these areas pertain to different cross sections along the downstream jet and their values may hence noticeably differ for the same valve [41, 49], they all show similar evolution in time, that can be compared. Finally, it is worthwhile observing that the above results also constitute an indirect (but robust) validation of the Δpnet analytical model.
4.1. Study Limitations
The ejection period rather than the entire systole is considered in the theoretical model of Δpnet. The model thus applies to positive flow rate (forward flow) only. However, the brief backward flow (Q(t)<0) that usually occurs in the late systole can be accounted for by substituting Q|Q| to Q2.
The ejection period, Tej and the open valve phase duration, Top are assumed equal when solving Equation (14), for the sake of simplicity. Notice that attributing a specific value to Top would be somehow arbitrary. However, additional calculations performed with Top=(1.05-1.2)Tej show that the correspondence of predicted in-vitro Δpnet can even improve with respect to the result shown in Fig. (5a).
Some assumptions (i.e., flat velocity profiles in the core of the transvalvular jet, length jet as a function of aortic area only rather than of the Reynolds number too) indirectly imply turbulent flow conditions. However, since transvalvular flow is typically recognized as transient [49] the adopted assumptions seems acceptable.
4.2. Future Developments
Ad-hoc in-vitro tests for comprehensive validation of both the Δpnet model and the EOA(t) computational tool are in progress. The quantities that are going to be monitored are Q(t), p1(t) and p2(t), and V1(t). The latter is necessary to estimate the experimental instantaneous effective orifice area as Q/(A.V1). High-speed video of the geometrical/projected orifice area will also be recorded, to compare time evolution of geometrical/projected/effective orifice area. Both bioprostheses and mechanical valves are planned to be tested, in order to analyse the ability of the model to describe transvalvular hemodynamics through ‘funnel type’ and non-circular, non-single orifices. Prostheses will also be artificially stenotized to examine main hemodynamic parameters (both predicted and experimental) as valve stenosis grade varies, when important valve dynamics effects are expected.
In-vivo application of the present theoretical approach is also planned, with two main aims: i) compare model and catheterization Δpnet; ii) deeply analyse the relationship between the tranvalvular drop routinely estimated by echocardiography to grade aortic stenosis and that predicted by the complete unsteady model. Both the above points are intended for a cohort of patients as large and various as possible. The idea is that provided point i) will give reliable results, point ii) will help in understanding sources and magnitudes of inconsistencies between guidelines and diagnostics, thus contributing to the improvement of aortic stenosis assessment.
CONCLUSION
Accurate and unique assessment of aortic stenosis by non-invasive quantification of hemodynamic parameters that consistently reflect ventricular overload is an open question yet. The net transvalvular pressure drop has been recognized as one of the markers that might help in closing the debate. The present analytical formulation of Δpnet(t) is proposed as a simple but complete tool that may be easily adopted in the clinical practice. The model requires only a limited number of data that can be acquired by routine echo-Doppler, and accounts not only for pressure loss and flow inertia contributions but also for transvalvular jet inertia effects due to valve leaflets movement. Model prediction is compared to in-vitro data and a satisfactory correspondence is found. In particular, the model turns out to reliably capture pressure drop oscillations due to valve dynamics. The present theoretical approach also provides a novel tool for the estimation of the instantaneous effective orifice area, which may be used in either in-vitro laboratories or catheterization rooms as an alternative to continuity equation.
ETHICS APPROVAL AND CONSENT TO PARTICIPATE
Not applicable.
HUMAN AND ANIMAL RIGHTS
No animals/humans were used for studies that are the basis
of this research.
CONSENT FOR PUBLICATION
Not applicable.
AVAILABILITY OF DATA AND MATERIALS
Not applicable.
FUNDING
The study was funded by the University of Padova PRAT grant (Code No: CPDA130215).
CONFLICT OF INTEREST
The author declares no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
The work was developed under the frame of the Infrastructure of Research of the University of Padova INCAS. The author acknowledges colleagues that participated in discussing the present research.
APPENDIX
The two integrals in equation (9) are evaluated as follows.
The first integral can be expressed as
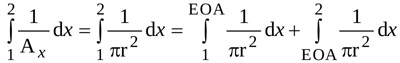 |
(1) |
where r=r(x,t) is the radius of the jet at location x and time t.
With notations as adopted in Fig. (1), the integral from location 1 to location EOA can be easily evaluated and expressed as
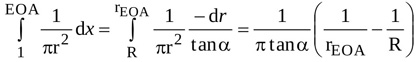 |
(2) |
where R and rEOA are the radius of the jet at locations 1 and EOA, respectively (i.e. at the LV outflow tract and at the vena contracta). The angle α is such that , where Lu is the length of the jet between locations 1 and EOA. Hence, equation (A2) can be rearranged as
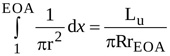 |
(3) |
The same approach applied to the integral from location EOA to location 2 in equation (A1) yields
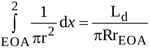 |
(4) |
where Ld is the length of the jet between locations EOA and 2.
Hence, the first integral in equation (9) is simply expressed as
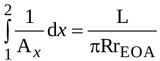 |
(5) |
where L=Lu+Ld is the total length of the jet.
The second integral in equation (9) can be written as
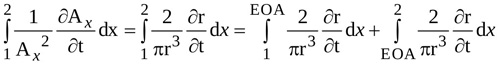 |
(6) |
The radius r of the jet between locations 1 and EOA is
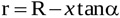 |
(7) |
so that the following relations hold
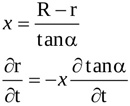 |
(8) |
Time variation of the length of the contracting jet, Lu is accounted for. Hence, the time derivative of the radius r is
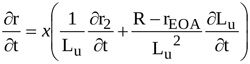 |
(9) |
With equations (A8) and (A9), the integral from locations 1 to EOA in equation (A6) can be written as
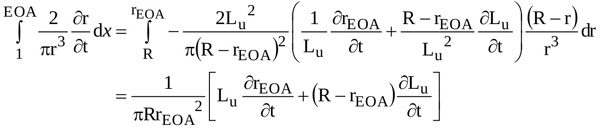 |
(10) |
A similar approach applied to the integral extended from EOA location to location 2 in equation (A6) yields
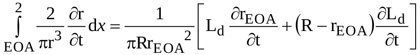 |
(11) |
Hence, the second integral in equation (9) reads
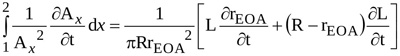 |
(12) |
Finally, with equations (A5) and (A12) and using the cross-sectional area instead of the radius, the local inertia term in equation (9) can be written as
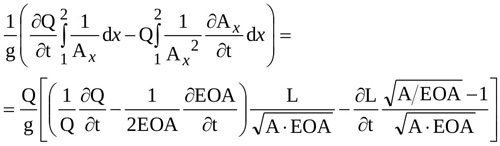 |
(13) |