All published articles of this journal are available on ScienceDirect.
Segmentation of Brain Tumor and Performance Evaluation Using Spatial FCM and Level Set Evolution
Abstract
Background:
In recent years, brain tumor is one of the major causes of death in human beings. The survival rate can be increased if the tumor is diagnosed accurately in the early stage. Hence, medical image segmentation is always a challenging task of any problem in computer guided medical procedures in hospitals. The main objective of the segmentation process is to obtain object of interest from the given image so that it can be represented in a meaningful way for further analysis.
Methods:
To improve the segmentation accuracy, an efficient segmentation method which combines a spatial fuzzy c-means and level sets is proposed in this paper.
Results:
The experiment is conducted using brain web and DICOM database. After pre-processing of an MR image, a spatial FCM algorithm is applied. The SFCM utilizes spatial data from the neighbourhood of each pixel to represent clusters. Finally, these clusters are segmented using level set active contour model for the tumor boundary. The performance of the proposed algorithm is evaluated using various performance metrics.
Conclusion:
In this technique, wavelets and spatial FCM are applied before segmenting the brain tumor by level sets. The qualitative results show more accurate detection of tumor boundary and better convergence rate of the contour as compared to other segmentation techniques. The proposed segmentation frame work is also compared with two automatic segmentation techniques developed recently. The quantitative results of the proposed method summarize the improvements in segmentation accuracy, sensitivity and specificity.
1. INTRODUCTION
In medical field, diagnosis and treatment planning completely depending on the various investigating techniques. These techniques provide very fast and accurate diagnostic results. In health care sector, medical imaging modalities, computer aided surgery techniques and artificial intelligence systems play an important role.
Among these modalities, medical imaging system remains the important diagnostic tool. By using this modality, the functioning of anatomical structures can be visualized and the surgery can be performed based on the 2-D or 3-D information through this mean. Nowadays, MRI (Magnetic Resonance Imaging) is popular and it has wide applications in the clinical radiology.
Segmentation is always the challenging task of any problem in computer guided medical procedures in hospitals. The main objective of segmentation process is to obtain the object of interest from the given image so that it can be represented in a meaningful way for further analysis. In medical field, segmentation process is applied to detect or localize the particular region of interest. The final outcome of this process is the partitioning of an image into its constituent parts which are representing the entire image [1]. Because of this reason segmentation plays a crucial role in medical image analysis. Generally, medical images are prone to noise and other artefacts due to patient movement and scanner resolution. Due to this, there is a low contrast and blurred edges in MR images [2]. In medical image segmentation, the object of interest is labelled as pixels and labelling of each pixel gives better clarity for the identification of a specific boundary or region in a medical image corresponding to the desired structure [3, 4, 5]. In recent years, brain tumor is one of the major causes for death in human beings. The survival rate can be increased if the tumor is diagnosed accurately in early stage. Most of the time, doctors treat patients for the strokes or brain haemorrhage instead of providing treatment for the tumor. Therefore, identification of the tumor is necessary to take further steps. Therefore, to increase the survival rate of the person who has a history of the brain tumor requires efficient medical image segmentation algorithms. There are many issues and challenges that help develop a unified approach to segment the brain tissues from MR images [6].
The proposed brain tumor segmentation technique uses spatial clustering and active contour models. In general, fuzzy segmentation method [7] is more beneficial and effective for the medical image segmentation. This method provides multiple clusters with variable degree of memberships based on the relationship between the pixels in an image. But the main disadvantage of this traditional FCM method is that, it is prone to noise and intensity inhomogeneity of the image. To overcome the limitations of traditional FCM, a spatial FCM algorithm is introduced to cluster tumors in the MR image. The extraction of the exact tumor boundary is carried out using active contour models. Towards improving the segmentation accuracy, this paper contributed an automatic brain tumor segmentation technique which is an unsupervised, fast and effective segmentation model which can be efficiently used in medical image processing field.
This paper is organized with the following contents. The related work pertaining to the proposed technique is reviewed in Section 2. The proposed methodology consisting of pre-processing, wavelet transform, a Spatial FCM and Active contour model i.e. Level set are discussed in Section 3. This section also includes the implementation of the proposed technique. The experimental results, performance evaluation of the proposed algorithm for various performance metrics and comparison of the proposed methodology with existing technique are presented in Section 4. The conclusion remarks are presented in Section 5.
2. RELATED WORKS
One of the significant and fast developing areas in clinical and diagnostic field is medical image segmentation. Automatic segmentation techniques [8] are classified and arranged to save time and human errors for segmenting anatomical structures of the brain. Because of the heterogeneous nature of the brain it is very difficult to analyze the brain disorder unless the efficient automatic segmentation process is carried out. In numerous segmentation algorithms, specialists need to utilize their insight and skill to alter the parameters identified with segmentation for an ideal performance.
The most popular technique imaging modality namely Magnetic Resonance Imaging (MRI) is used to generate 2-D visual representation [9] of the affected region in the human brain. The MRI technique is the latest imaging modality that provides more details of the brain tissue structures and the anatomy of the soft tissues in human brain. In semi-automatic segmentation techniques, the doctors instate the segmentation and interfere with the procedure as and when required. Hence, these techniques may offer inaccuracy and time consuming. To overcome these drawbacks automatic segmentation methods are introduced. In order to establish the best segmentation technique which is user friendly automatic segmentation systems is often used in the field of medicine. To realize the advancement in automatic segmentation techniques used to segment the brain tumor from MRI, a brief literature survey is provided. The FCM (Fuzzy C-Means) technique has been playing an important role in automatic segmentation techniques. This technique has limitations as it is very sensitive to noise and intensity inhomogeneity of the images. Also, the optimization is very insignificant because of its poor initialization process. Recently, many modified FCMs methods have been introduced combining with active contour models. The FCM technique [10] uses spatially constrained membership functions adaptively for optimization. This method results in poor segmentation accuracy due to its selection of local membership functions. The FCM algorithm is modified by incorporating spatial details in the existing FCM algorithm [11], similarity measure can be drawn to a pixel closer to the cluster centre through computation. This may be carried out for homogeneous region. The main draw back in this method is segmenting clusters to detect the exact tumor boundary.
Ahmed et al. [12] developed an algorithm by introducing local grey level details. This is done by altering the objective function with one more similarity measure for the estimation of bias field and segmenting of tumor from MR images. Segmentation of tumors by the application of K-means, EM and Normalized graph cuts algorithms have been introduced in another study [13]. In this paper, they have analysed the two previous automatic segmentation methods and comparative analysis have been carried out with a normalized graph cut method. Then, partitioning algorithm is applied for grey scale images by varying k values i.e. number of clusters. In this method, it is noticed that, for small values of k, this method performs better and increased values of k, the performance is poor. Also, multiple number of clusters appear at different locations of the image. Hence, the Normalized Cuts (NC) method produces better results for higher values of k by taking more time for computation.
Wilson and Dhas [14] have applied K-means and FCM algorithms to segment and extract the brain tumor from MR image. The primary weakness of their technique is that they have not combined these two methods which can produce better results. To overcome this issue, Rao et al. [15] presented an unsupervised technique to segment the brain tumor by applying a conditional random field approach.
A technique to detect the brain anomalies using the binarization process is proposed in a study [16]. This uses statistical features of the image namely variance, mean, standard deviation and entropy. This technique is fast and simple to run the large datasets but unable to detect complete tumor boundary. There are algorithms recently introduced and they work based on the artificial intelligence and machine learning [17, 18].
Another technique which is fully automatic was introduced in a study [19] for the segmentation of brain tumor. This methodology is very efficient and uses the combination of Gaussian Mixture Model (GMM) and FCM. The main drawbacks of this technique are that it is prone to noise and blurred edges of the image. Also, it is computationally intensive.
To overcome the limitations incurred in the above techniques, a new segmentation technique based on the spatial FCM and level sets is introduced in the proposed methodology.
3. PROPOSED METHODOLOGY
In medical image segmentation techniques, k-means clustering algorithms are commonly used to detect the brain tumors. It is observed that, the K-means algorithm is very much useful to run the large datasets with faster rate. But, it shows poor detection ratio for tumors which are blurred in nature. Other systems based on Fuzzy C-Means algorithms maintains strong detection ratio while retaining the information in the original image. This helps to identify cancerous cells correctly as compared to the k-means algorithms. But, the main issue is that, they are very sensitive to noise and other artefacts. To overcome these drawbacks, modified FCM known as a spatial FCM clustering is proposed. This algorithm is advantageous in terms of Euclidian distance calculation and optimal cluster initialization. This section presents the methodology applied to extract brain tumor from the given MR image. The brain tumor extraction steps include image pre-processing, clustering of tumors and segmentation of tumor clusters by level set method, which are depicted in (Fig. 1).
3.1. Pre-processing Stage
Medical images prone to background noise and artefacts. To improve the segmentation accuracy, the quality of the input image should be improved by pre-processing technique. The proposed pre-processing stage consists of median filtering and multiresolution analysis of the filtered image using wavelet transform [20, 21].
3.1.1. Median Filtering
For medical image processing, non-linear filters are the most preferred choice than linear filters for removingthe noise present in the medical images. Median filter [22] is a nonlinear filter used to eliminate noise present in the image while retaining edges information. Median filter performs by moving pixel by pixel through the image, replacing each pixel value with median value of neighbouring pixels. In this filter, window is chosen in such a way that it slides every pixel one by one on the whole image. The median is determined by first arranging all the pixel from the window into numerical order and after that supplanting the pixel being considered with the centre (median) value of the pixel. The output of the median filter is free from noisy MR image which can be utilized for the next processing stage of segmentation.
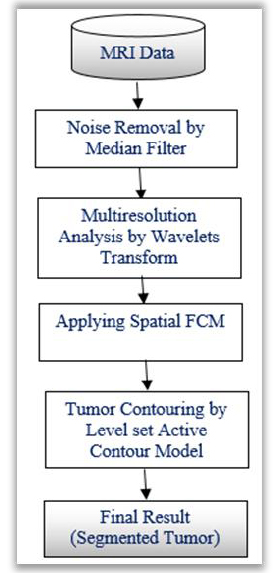
3.1.2. Multiresolution Analysis
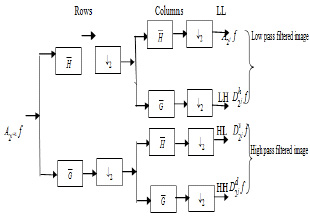
Multiresolution analysis is commonly used in medical image segmentation for de-noising the original image. The multiresolution analysis of wavelets provides a better characterization for non-stationary signal characteristics namely blurred edges, spikes and orientation. The enhancement of the filtered image can be described into multiple resolutions by applying suitable wavelet transform.
This procedure makes the next level i.e. advanced processing and analysis. Wavelets can be viewed as projection of the image on a required set of scaling. Notion of scale is important in the analysis and extraction of details from the image. The multiresolution and wavelet representation in 2-D scale is shown in Fig. (2).The wavelet model can be applied to 2-D images by separable multiresolution approximation L2(R2) with scaling function 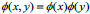 .
.
There are three associated wavelet functions 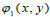
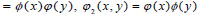 and
and 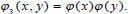 The 2-D image decomposition can be computed using 1-D decomposition algorithm by making use of separable property of the wavelet transform. The image
The 2-D image decomposition can be computed using 1-D decomposition algorithm by making use of separable property of the wavelet transform. The image 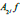 is the course approximation at the resolution 2j and the images
is the course approximation at the resolution 2j and the images 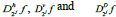 provide detailed information for different orientations and resolutions. If the input image consists of N number of pixels, then each of the images will have 2jN pixels so that the total number of pixels in this new representation is equal to the number of pixels of the input image to keep the volume of data maintained.
provide detailed information for different orientations and resolutions. If the input image consists of N number of pixels, then each of the images will have 2jN pixels so that the total number of pixels in this new representation is equal to the number of pixels of the input image to keep the volume of data maintained.
3.2. FCM Clustering
Before discussing spatial FCM, let us understand the traditional FCM. This algorithm works on the basis of minimization of a quadratic criterion in which the clusters are indicated with their corresponding centres. For the case of segmentation process using fuzzy membership, it allocates pixels to each category. The FCM technique is first introduced by Bezdek [23]. By the application of Fuzzy membership, FCM algorithm assigns pixels to each category.
Consider X = (X1,X2,.....XN ) represents an image with N pixels to be segmented into c clusters, in which xi indicates features data. Here, FCM allows partitioning of an image into its constituent parts in terms of pixels by iteratively finding the centres of clusters, vi and the membership matrix, U through minimizing an objective function JFCM with respect to these cluster centers and membership values can be defined as equation (1).
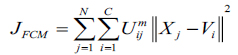 |
(1) |
here, Uij represents pixel membership xj in the jth cluster and vi becomes ith cluster center.
The value of m responsible for partition due to fuzziness and the cost function is minimized as centroid close to the pixels. Therefore, pixels near to centroid assigned as high membership values and low membership values for the data too away from the centroid. Hence, there is a probability of pixels belonging to that particular cluster membership function. In FCM techniques, the probability depends entirely on the distance between every individual cluster centre and pixels in the feature domain. The cluster centers and membership functions are updated by applying the expression given in Equation (2) and (3).
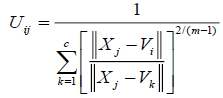 |
(2) |
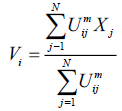 |
(3) |
The convergence process occurs with the clusters and change in membership function for every two steps of iterations.
3.3. Spatial FCM
Proposed segmentation process mainly involves classifying intensities of pixels into non-overlapping homogeneous groups. MR images with intensity inhomogeneties have strong correlation with neighbouring pixels especially in the edges of the tumor. The probability belongs to the same cluster group based on the pixels which possess similar feature values. Obtaining these spatial characteristics which is very significant for correct formation of clusters is not exploited in traditional FCM technique. Therefore, to make use of these spatial details, a spatial function is formulated as given in the following function.
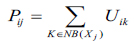 |
(4) |
here, Pij indicates the probability that pixel Xj belongs to ith cluster NBjx is square window which centre on pixel xj in spatial domain. In this algorithm 5X5 window is used. The probability function defined in Equation (4) is included in fuzzy membership function to generate a new membership values for every pixel provided the adjacent pixels provides similar information and the pixel which is at centre must have higher probability of grouping to the same cluster as of the adjacent pixels. The spatial function with incorporation of membership function is given in the following equation (5).
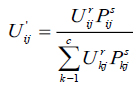 |
(5) |
here, r and s values controls the relative importance of both functions. In case of the homogenous region, the spatial information functions simply fortify the original membership, function and there is no change in the clustering results. The spatial FCM with parameter r and s is denoted Spatial as FCMr,s. It is noticed that, FCM1,0 is similar to that of traditional FCM technique. The clustering has two steps for every two iterations. In the first step traditional FCM is used to compute the membership function in spectral domain. The second step involves the mapping of spatial information of each pixel to the member function. Then FCM iteration proceeds with the new membership function that included with a spatial information. The iteration is stopped whenever the threshold value is less between the maximum values of cluster centers for every two successive iterations. Once it converged, the de-fuzzification is initiated to assign each pixel to a particular cluster where the membership value is maximum.
3.4. Level Sets Evolution
After applying a spatial FCM, the tumor boundary can be detected by using level set active contour model. The tumor is the connected points of sharp change in a region of an image where pixel locations have abrupt intensity variations i.e. a discontinuity in grey level values. To segment such tumor boundary a robust segmentation method is required. Active contour models show such capabilities to segment brain tumor as compared to other segmentation techniques. The proposed methodology makes use of level sets [24] for contouring the tumor boundary from MR image. The level set technique is based on the active contour models which offers energy minimization of the contour. An active contour is made up of a set of points at instant time and it is expressed as, equation (6).
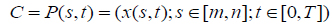 |
(6) |
here, m and n are limits of the curve. The energy minimization of the curve is defined as, equation (7)
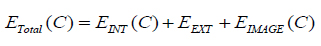 |
(7) |
The segmentation applying level set uses energy minimization of active contour [25, 26] surfacing in one higher 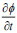 dimension. In this case, the evolving surface is
dimension. In this case, the evolving surface is 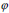 in place of contour C. In this technique, the curve C(s) is represented by
in place of contour C. In this technique, the curve C(s) is represented by 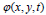 as an implicit function and the front is expressed implicitly as
as an implicit function and the front is expressed implicitly as 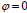 . It is called as level set. Given an initial surface
. It is called as level set. Given an initial surface 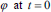 it would be necessary to have
it would be necessary to have  at any time i expressed using a chain rule as, (Eq. 8-10)
at any time i expressed using a chain rule as, (Eq. 8-10)
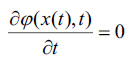 |
(8) |
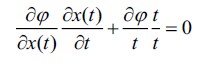 |
(9) |
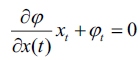 |
(10) |
here,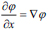 and xi is the speed given by the force F normal to the surface, then xt = F(x(t))n here,
and xi is the speed given by the force F normal to the surface, then xt = F(x(t))n here, 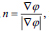 now equation (10) can be rewritten as, (Eq. 11-14)
now equation (10) can be rewritten as, (Eq. 11-14)
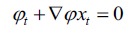 |
(11) |
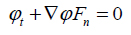 |
(12) |
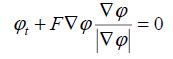 |
(13) |
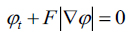 |
(14) |
Equation (14) can be applied for the contour evolution with the level set function The parameter F is called the speed function 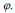 The function F depends on image information as well as the value of
The function F depends on image information as well as the value of 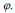
4. EXPERIMENTAL RESULTS AND DISCUSSION
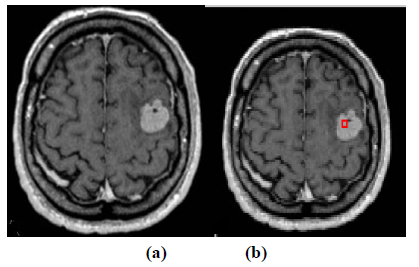
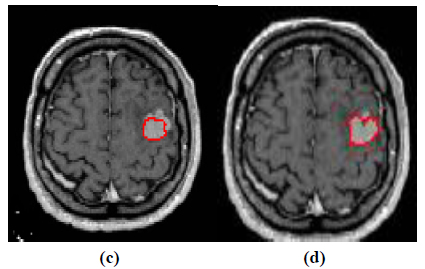
The experiment is conducted using brain web and Digital Imaging Communications in Medicine (DICOM) database [27, 28]. These database consists of T2 weighted MR images of sizes with tumor history. Pre-processing of an original MR image is an important step before applying the segmentation algorithms. In this case, the original MR image is pre-processed by applying median filter. Median filter removes salt and pepper noise which is very common in MR images of the brain. After removing the noise, wavelet transform is applied for multiresolution analysis to enhance the features of the image. Then, spatial FCM technique is applied to the multiresolution image. This technique minimizes search area to a very small region by creating cluster number k parameter for termination and max iteration values. Finally, these tumor clusters are segmented by level set evolution algorithm [29-39]. The following experimental results demonstrate the segmentation process used in the proposed methodology. In this experiment, two MR images having tumor in different locations of the image were selected to test the proposed segmentation algorithm. In Fig. (3), the original image and contour initialization for MR image 1 is shown. The contour evolution and final segmentation are depicted in Fig. (4). Similarly, Fig. (5) shows the original MR image 2 and the initial contour position. As the iteration values increases, the contour evolves towards the tumor boundary.
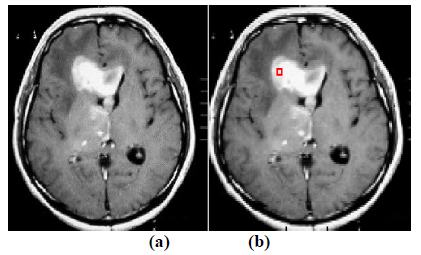
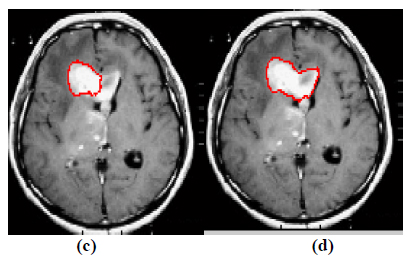
The qualitative results of the proposed method show that, the convergence of the contour towards the object boundary is very accurate and rate of convergence of the contour using level sets method is better than the traditional active contour models. The quantitative analysis is also carried out for the proposed technique using various performance measures.
In this method, Dice and Jaccard coefficients are used to find the overlap between two segmented output and ground truth (Eq. 15-18).
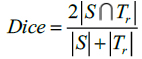 |
(15) |
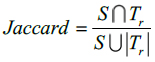 |
(16) |
Here, S indicates the segmented image from the proposed Fr method and indicates the ground truth of the given MR image. The segmented images are converted to binary images by suitable thresholding. In this case, ‘0’ represents overlaps between the output image and the ground truth and ‘1’ indicates congested values between them.
The performance of the proposed method is also evaluated by using Sensitivity and Specificity which are defined as,
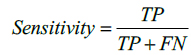 |
(17) |
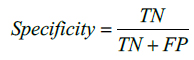 |
(18) |
here, TP indicates True Positive and TN represents True Negative. Similarly, FP and FN represents False Positive and False Negative respectively. Tables 1 and 2 illustrate the segmentation performance for the MR image 1 and MR image 2 respectively.
CONCLUSION
In this paper a spatial FCM and Level set evolution method is proposed to segment the brain tumor from MR images. The experiment was carried out using bench mark database. The performance of the system is evaluated with various performance measures. The qualitative and quantitative results obtained in this method are discussed in detail. The values of Dice and Jaccard coefficients proves the improvements in accurate segmentation of brain tumor. The proposed segmentation frame work is also compared with two automatic segmentation techniques developed recently. It is evident from the comparative analysis, the proposed method of segmenting brain tumor is more accurate as compared to the other techniques.
LIST OF ABBREVIATIONS
| MRI | = Magnetic Resonance Imaging |
| SFCM | = Spatial Fuzzy-c Means |
| GMM | = Gaussian Mixture Model |
ETHICS APPROVAL AND CONSENT TO PARTICIPATE
Not applicable.
HUMAN AND ANIMAL RIGHTS
No animals/humans were used for studies that are the basis of this research.
CONSENT FOR PUBLICATION
Not applicable.
AVAILABILITY OF DATA AND MATERIALS
Not applicable.
FUNDING
None.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
Declared none.


